Beth Chance, Nathan Tintle, and the ISI team

Although we strongly agree that we must do more to help students understand the role of sampling variability in inferential decisions, we have not yet been convinced that a formal treatment of bootstrapping (having students sample with replacement) is the only path to get them there.[pullquote]we worry that the motivation for conducting bootstrapping is less intuitive for students[/pullquote]

Our curriculum begins by introducing students to inference about a single proportion. We start with tests of significance. Students ask ‘what if the null hypothesis is true,’ which models the underlying logic of statistical inference. The ‘what if’ question is answered by having students simulate different values of the sample proportion that could occur if the null hypothesis was true. Students look at the shape and center of the resulting simulated “null distribution,” but we quickly transition to the fact that what is most important about this distribution is its variability.That variability helps us decide whether our observed statistic is in the tail of the distribution, giving us a sense of the plausibility of the null hypothesis. To generate a confidence interval, students ask a series of systematic ‘what if’ questions – changing the null hypothesis parameter value each time. If the observed  is not a surprising value in the resulting sampling distribution, then the population proportion yielding that distribution is considered plausible. Students can use this approach to quickly generate a range of plausible values for the unknown parameter.

Creating an interval of plausible values from ISI text

Student then explore other “short-cut” methods for estimating the standard deviation of the null distribution, such as using 0.5 in the traditional formula for the most conservative estimate.

In this context, bootstrapping would generate a sampling distribution centered at the observed sample proportion. But, we worry that the motivation for conducting bootstrapping is less intuitive for students (it doesn’t match the core logic of inference). In fact, we wonder if it is reinforcing the frequent introductory statistics student misconception that the null hypothesis is about the observed statistic, not the unknown parameter, or that the confidence interval is about the sample statistic rather than the population parameter.

Though we find our approach natural and straightforward to introduce tests and confidence intervals for a single proportion, where do we go from here? For example, what do we have students do when the statistic is a sample mean?  First, we give them a hypothetical population to sample from (click image below to enlarge).  Why is this better than having them take repeated samples from the observed sample, as is the case with bootstrapping? Our intuition is that somehow this is more concrete for students and helps emphasize the logic of statistical inference, much as we argued above for a single proportion.

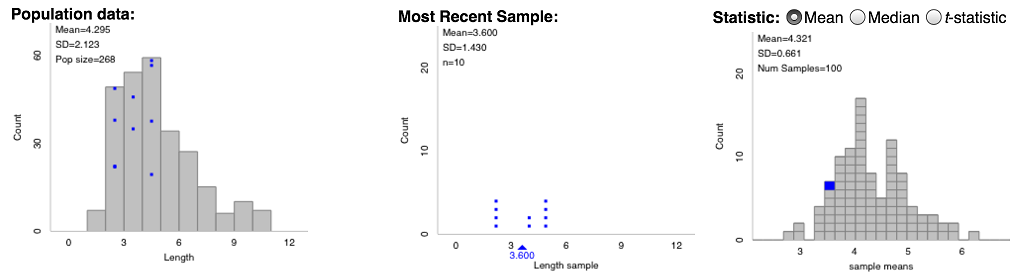One hundred samples of size 10 recording word lengths of words in the Gettysburg Address

Students explore different hypothetical finite populations to come to the conclusion that the shape of the population is less the issue in determining the sampling distribution of the mean, but rather the variability in the sample and the sample size are the crucial pieces of information. In fact, with a sample mean, we see no reason to not use the usual standard error formula s/ .  Once they are convinced (empirically) that formula works, they can proceed to standardized statistics and informal confidence intervals ( + 2SE, similarto Karsten’s approach but with different methods for estimating the standard error), always focusing on determining plausible values for the unknown population mean.  We advocate getting students comfortable with “2 SE,” rather than dealing with some of the complications and “fixes” needed for bootstrap intervals to work well.

To us, the real advantage of bootstrapping comes when you want to use a statistic other than the sample mean, like the sample median. However, bootstrapping does not work well when you have a “one observation statistic” like the median.  (See Tim’s post for other situations where the bootstrap may not work “better.”) Still, we feel that any approach that gets students asking such questions and feeling they have the power to change the statistic and how they would proceed is worthwhile!

Moving on to comparing groups, you do have the question of whether the simulation should sample with replacement (mimicking the random sampling process) or without replacement (mimicking the random assignment process).  For simplicity, our current approach is to always use the latter.  This makes it very easy for students to change statistics and focus on chance variation, without all the “baggage” of bootstrapping.  [pullquote] This makes it very easy for students to change statistics and focus on chance variation, without all the “baggage” of bootstrapping. [/pullquote]Students still must consider the sampling design when drawing their final conclusions but in the introductory course, we are happy if they can explain why a result is or is not plausible by random chance alone. In a follow-up course they can focus more on the actual source of the random chance and how that impacts the analysis.

We think several approaches may be viable and more classroom-based research is needed to better understand the different options and which one(s) may be best. In fact, many of our arguments are similar to those made by folks using bootstrapping. As Chris said, the main thing is to focus on our goals when teaching confidence interval and do our best to match them with students’ goals and intuition.  Not introducing bootstrapping is one area where we have simplified the details in an attempt to focus on the bigger picture of statistical inference.