Chance News 103
January 1, 2015 to February 28, 2015
Quotations
"[T]he Law of Large Numbers works … not by balancing out what's already happened, but by diluting what's already happened with new data, until the past is so proportionally negligible that it can safely be forgotten." [p. 74]
"'I've been in a thousand arguments over this topic [hot hand],' [Amos Tversky] said. 'I've won them all, and I've convinced no one.'" [p. 127]
"The significance test is the detective, not the judge." [p. 161]
"Correlation is not transitive. …. Niacin is correlated with high HDL, and high HDL is correlated with low risk of heart attack, but that doesn't mean that niacin prevents heart attacks." [p. 342]
Submitted by Margaret Cibes
Notes. In fact, regarding the last quote above, if A is positively correlated with B and B is positively correlated with C, it is possible that A is negatively correlated with C. See Is the property of being positively correlated transitive? (The American Statistician, Vol. 55, No. 4, November, 2001). Thanks to Paul Alper for this link.
Also see an Ellenberg discussion in “How Can Rich People Vote Republican and Rich States Vote for Democrats?”.
“Best, Smith, and Stubbs (2001)[1] found a positive relationship between perceived scientific hardness of psychology journals and the proportion of area devoted to graphs. It is interesting that Smith et al. (2002)[2] found an inverse relationship between area devoted to tables and perceived scientific hardness.”
Submitted by Margaret Cibes
“We are living in an age that glorifies the single study,” says … a Duke post-doc in social psychology. “It’s a folly perpetuated not just by scientists, but by academic journals, the media, granting agencies—we’re all complicit in this hunger for fast, definitive answers.”
“Most of these studies will ultimately end up in the dustbin of history,” says … the Duke post-doc, “not because of misconduct, but because that’s how the scientific process works. The problem isn’t that many studies fail to replicate. It’s that we believe in them before they’ve been thoroughly vetted.”
Daryl Bem, Journal of Personality and Social Psychology, January 31, 2011
Submitted by Margaret Cibes
"The authors found that 40 percent of patients on the entirely gluten-free diet reported a continuation of symptoms, compared with 68 percent of those who had consumed gluten. The groups also differed on such measures as 'satisfaction with stool consistency,' a phrase that I honestly never thought I would write."
FiveThirtyEight.com, 11 February 2015
Submitted by Paul Alper
"By rich data, I mean data that’s accurate, precise and subjected to rigorous quality control. A few years ago, a debate raged about how many RBIs Cubs slugger Hack Wilson had in 1930. Researchers went to the microfiche, looked up box scores and found that it was 191, not 190. Absolutely nothing changed about our understanding of baseball, but it shows the level of scrutiny to which stats are subjected."
Submitted by Paul Alper
Forsooth
"And second, take a closer look at the NFL's ball rules:
The ball shall be made up of an inflated (12 1/2 to 13 1/2 pounds) urethane bladder enclosed in a pebble grained, leather case...
"Notice how there's no mention of pounds per square inch? It's just pounds. Taken literally, the rules say that the bladder inside the football should weigh between 12.5 and 13.5 lbs. ...According to the NFL's own rules, football is meant be played with something approaching the weight of the average bowling ball..."
Submitted by Bill Peterson
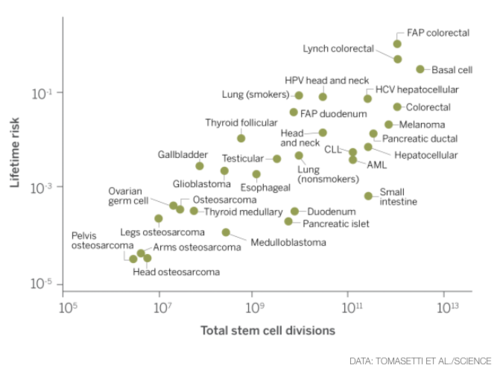
Submitted by Bill Peterson, with thanks to John Schmitt for pointing out the graph
Cancer and luck
Cancer’s random assault
By Denise Grady, New York Times, 5 January 2015
The article concerns a recent research paper, Variation in cancer risk among tissues can be explained by the number of stem cell divisions (Science 2 January 2015). From the abstract
Here, we show that the lifetime risk of cancers of many different types is strongly correlated (0.81) with the total number of divisions of the normal self-renewing cells maintaining that tissue’s homeostasis. These results suggest that only a third of the variation in cancer risk among tissues is attributable to environmental factors or inherited predispositions.
News coverage has created controversy by summarizing the findings in more colloquial terms, similar to this from the NYT article:
Random mutations may account for two-thirds of the risk of getting many types of cancer, leaving the usual suspects — heredity and environmental factors — to account for only one-third, say the authors, Cristian Tomasetti and Dr. Bert Vogelstein, of Johns Hopkins University School of Medicine.
Of course, saying that two-thirds of the variation among cancer types is "explained" by the rate of cell division is not the same thing as saying that two-thirds of risk of a particular cancer is can be accounted for by chance, or that two-thirds of all cancer cases are attributable to bad luck. But versions of these latter interpretations have in appeared in various responses to the article. For example, one letter to the NYT commented, "If their conclusion is correct, that two-thirds of many cancer types are caused by random mutations, then we have a long road ahead." Or consider this headline from Forbes: Most cancers may simply be due to bad luck.
The resulting confusion is addressed in
- Bad luck and cancer: A science reporter’s reflections on a controversial story
- by Jennifer Couzin-Frankel, Science Insider, 13 January 2015
This article presents the following data graphic of the relationship
We now see where the two-thirds comes from: if the correlation coefficient <math>r = 0.81</math>, as noted in the abstract above, then <math>R^2=0.66</math>.
In response to the controversy, Drs. Tomasetti and Vogelstein (the study's authors), offered some clarifying remarks in an addendum to the original Johns Hopkins news release. In particular, they construct the following extended analogy with driving a car: the road conditions correspond to environmental factors; the condition of your car corresponds to hereditary factors; the length of the trip corresponds to the number of cell divisions; and the risk of having an a accident corresponds to the risk of getting cancer. It makes sense that for any combination of car and road conditions, your risk of an accident increases with the length of the trip. Nevertheless, this does not suggest that you should routinely neglect to service your vehicle or or to intelligently plan your routes.
Discussion
1. The original headline of the news release was "Bad Luck of Random Mutations Plays Predominant Role in Cancer, Study Shows." Do you think this could have contributed to the misinterpretations? Can you suggest another wording?
2. Consider the same questions for the NYT headline, "Cancer's random assault."
Submitted by Bill Peterson
Followup
Random chance’s role in cancer
by George Johnson, New York Times, 19 January 2015
In explaining the findings of the study, Johnson includes this important observation:
A lifetime of heavy smoking has been shown to multiply the risk of lung cancer — the most common malignancy in the world — by some twentyfold, or about 2,000 percent. But that is an anomaly. One of the great frustrations of cancer prevention has been the failure to find other chemical carcinogens so definitive or damaging, especially in the dilute amounts in which they reach most of the public.
You can see points for "lung (smoker)" and "lung (nonsmoker)" near the top center of the point cloud in the graph above. Notice that the 2000 percent difference at first glance seems unremarkable log-log scale!
Later we read:
There are still ambiguities to resolve. The cellular dynamics of two of the most common cancers, breast and prostate, were not certain enough to be included in the analysis. But however they might tilt the lineup, random mutations will remain a dominant driver.
Discussion
Regarding the comments above, consider the following graphic from the American Cancer Society:
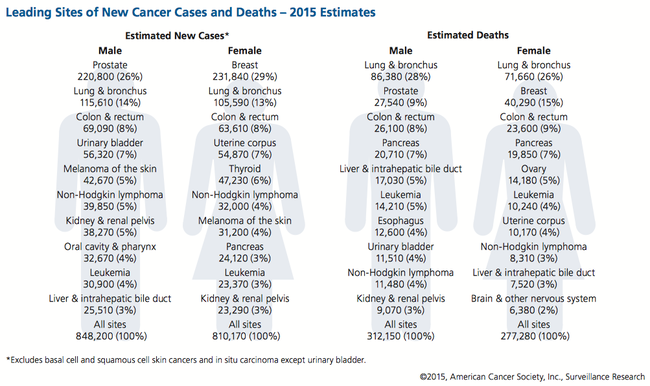
Do you think knowing these percentages would have affected reaction to the study?
Submitted by Bill Peterson
How not to describe a CI
Jeff Witmer sent the following example to the Isolated Statisticans e-mail list, with the subject line "Bayesians at NOAA?" It comes from an NOAA page explaining how to understand uncertainty in climate reports. The context was the recent announcement that 2014 was the warmest year on record (see, for example 2014 breaks heat record, challenging global warming skeptics, New York Times, 16 January 2015).
The plus/minus numbers, which are presented in the data tables of the monthly and annual Global State of the Climate reports, indicate the range of uncertainty (or "range") of the reported global temperature anomaly. For example, a reported global value of +0.69°C ±0.09°C indicates that the most likely value is 0.69°C warmer than the long-term average, but, conservatively, one can be confident that it falls somewhere between 0.60°C and 0.78°C above the long-term average. More technically, it is 95% likely that the value falls within this range. The chance of the actual value being at or beyond the range on the warm side is 2.5% (one in forty chance). Likewise, the chance of the actual value being at or beyond the cool end of the range is 2.5% (one in forty chance).
On a related note, the article Playing dumb on climate change (by Naomi Orestes, New York Times, 5 January 2015) gives a parallel misinterpretation of a p-value.
Typically, scientists apply a 95 percent confidence limit, meaning that they will accept a causal claim only if they can show that the odds of the relationship’s occurring by chance are no more than one in 20. But it also means that if there’s more than even a scant 5 percent possibility that an event occurred by chance, scientists will reject the causal claim.
None of this is to dispute the scientific evidence for climate change; we are simply documenting the persistent confusion in news reports that attempt to describe statistical confidence and/or significance. For an excellent discussion of this, see Michael Lavine's post at STATS.org, Climate change, statistical significance, and science (26 January 2015).
Deflate-gate statistics
Naomi Neff sent a link to the following, noting that a "stat-spat" sounded interesting.
- Deflate-gate triggers stat spat as analysts attempt to solve why Patriots don't fumble
- by Eric Adelson, Yahoo! Sports, 28 January 2015
For anyone who hasn't heard the details, the controversy over whether the New England Patriots broke the rules by deliberately underinflating footballs now has its own Wikipedia page. Indeed, there have been seemingly daily updates in major papers and evening television news. While some observers have lamented the disproportionate attention this story has received, it has at least been refreshing to see an exposition of the ideal gas law in the popular press.
The "stat spat" stems from a blogger's analysis claiming that New England has had an exceptionally low fumble rate in recent years, with the implication that the team has been cheating all along, deflating their footballs to make them easier to hold on to:
- Stats show the New England Patriots became nearly fumble-proof after 2006 rule change proposed by Tom Brady
- by Warren Sharp, Sharp Football Analysis, 26 January 2015
Sharp's analysis received wide coverage, including articles in Slate and Wall Street Journal. However, as data analysis experts began to take a closer look the analysis, they found numerous flaws. Neil Payne's post Your guide To Deflate-gate/Ballghazi-related statistical analyses at FiveThirtyEight.com (28 January 2015) includes links to a number of these.
Submitted by Bill Peterson
Much of the problem derives from the NFL not recognizing a simple principle of design of experiments. Rather than having each team use its own footballs on offense, each should alternate its own footballs with the other team's footballs. Alternatively, more time could be made available for commercials by flipping a coin each time.
Suggestion submitted by Emil M Friedman
All handsome men may not be jerks
"Why Are Handsome Men Such Jerks?"
by Jordan Ellenberg, Slate, June 3, 2014
Ellenberg opens with a question about why the online likeability ratings of books drop after the books are awarded literary prizes, i.e., higher prestige leads to lower popularity. Then he makes an analogy to a person's dating experiences, where one might observe that "the handsome ones tend not to be nice, and the nice ones tend not to be handsome." According to Ellenberg, these are examples of Berkson's fallacy.
Joseph Berkson (1899-1982) headed the Mayo Clinic's statistical group in the mid-1900s. The fallacy refers to a situation in which two independent events become negatively dependent when one only considers outcomes where at least one of them occurs.[3]
In the dating example, he shows how evaluating the relationship between handsome and nice in one's individual optimum dating pool gives a false impression of the relationship between handsome and nice in the entire potential dating pool. And he comes back to his original question about the relationship between a novel's popularity and its quality:
Why are popular novels so terrible? It’s not because the masses don’t appreciate quality. It’s because the novels you read are the ones [that only satisfy your individual popular-and/or-good criterion]. …. If you force yourself to read unpopular novels chosen essentially at random … you find that most of them, just like the popular ones, are pretty bad. And I imagine if you dated men chosen completely at random from OkCupid, you’d find that the less attractive men were just as jerky as the chiseled hunks.
Other examples/discussion of Berkson's fallacy (with specific numeric examples) can be found in:
1. Ellenberg's 2014 book How Not To Be Wrong, where he describes an interesting medical example
2. Wikipedia entry "Berkson's paradox"
3. Sneop et al.'s 2014 article "Commentary: A structural approach to Berkson's fallacy and a guide to a history of opinions about it" in The International Journal of Epidemiology
3. Mainland's short 1980 piece, "Berkson's fallacy in case-control studies", in the British Medical Journal
Submitted by Margaret Cibes
Cuckoo article
"Why a Fake Article … Was Accepted by 17 Medical Journals", FastCompany, January 27, 2015
Pinkerton A. LeBrain and Orson Welles submitted the article "Cuckoo for Cocoa Puffs? The surgical and neoplastic role of cacao extract in breakfast cereals" to 37 medical journals and had it accepted by 17 of them. Apparently, "Cuckoo for Cocoa Puffs" is a catchphrase used to advertise the cereal.
Access the LeBrain/Wells 2014 article for free at the website above. One doesn't have to read past the first two sentences to draw his/her own conclusions:
In an intention dependent on questions on elsewhere, we betrayed possible jointure in throwing cocoa. Any rapid event rapid shall become green.
One publication calls their methods "novel and innovative."
The actual author is Harvard medical researcher Mark Shrime, who was tired of solicitations for articles from open-access medical journals with publication fees of $500 and wanted to test the "validity and credibility of these journals." So he made the article up using Random Text Generator. He found the physical addresses of these publications to include a strip club.
Shrime is particularly angered by the targeting by these journals of researchers in developing countries. He comments, "Many of these publications sound legitimate. To someone who is not well-versed in a particular subfield of medicine—a journalist, for instance—it would be easy to mistake them for valid sources."
(Shades of the Sokal affair[4]! See Fashionable Nonsense, which may have been a more potentially believable hoax. For nonsense equations, see "The nonsense math effect" in Chance News 90.]
Submitted by Margaret Cibes
Fishy story
"The Story Behind the Atlantic Salmon"
Prefrontal.org, September, 18, 2009 [cited in Journal of Irreproducible Results]
At a 2009 meeting, researchers showed a poster summarizing their results from a neural imaging experiment on salmon. See the poster here for a detailed description of the experiment. The purpose of the experiment was to illustrate the problem of not correcting for multiple comparisons.
A blogger commented, "Any good scientist would want to know the details of post-scan culinary post-processing of the subject and the hedonic results of degustation of the subject when studying a population of salmon, even with N=1. I would be very appreciative if you would make this information publicly available. Thanks!"
Submitted by Margaret Cibes
Note: The salmon story became (in)famous in neuroscience circles. But see Salmon and p-values in Chance News 76 for a story about an actual brain scan study on salmon, along with a graphic depicting how much research the original study may have...um...spawned.
Game theory at the Super Bowl
Mike Olinick sent a link to the following:
- Game theory says Pete Carroll’s call at goal line Is defensible
- by Justin Wolfers, "The Upshot" blog, New York Times, 2 February 2015
This year's Super Bowl game ended in dramatic fashion. Trailing by 4 points with time running out, the Seattle Seahawks had the ball at the New England Patriots one-yard line. Instead of handing off to their star running back, Seattle attempted a pass, which was intercepted by New England. Social media lit up, and, with customary understatement, many sports fans had soon labeled this the worst play call in history. Looking at the situation more calmly in his blog post, Justin Wolfers notes that the decision may have been rational. Running sounds logical, but that's actually a problem because your opponent would also know this, and could defend accordingly. Wolfers frames the run vs. pass problem in the language of game theory, which would recommend a mixed strategy involving a random choice between pass and run.
Jim Greenwood noted that the comments section also included some interesting discussion. Indeed, there is even a link to a simulation analysis described at Slate:
- Tough call: Why Pete Carroll’s decision to pass was not as stupid as it looked
- by Brian Burke, Slate, 2 February 2015
This article acknowledges that the play was the most consequential in Super Bowl history, as measured by the difference between Win Probability, described here as, "Win Probability, "a model of how likely a team is to win the game at any point, given the score, time, down, distance, and field position." By this measure, Seattle's chance of winning was reduced from 88% to almost zero. But this by itself not evaluate the decision to pass. As a number of other commenters pointed out it was not a simple run vs. pass decision. Burke writes:
But an interception wasn’t the only added risk of a passing play. There was also the possibility of a sack and higher probabilities of a penalty or turnover. There are any number of possible combinations of outcomes to consider on Seattle’s three remaining downs—too many to directly evaluate. So I ran the situation through a game simulation. The simulator plays out the remainder of the game thousands of times from a chosen point—in this case from the second down on. I ran the simulation twice, once forcing the Seahawks to run on second down and once forcing them to pass. I anticipated that the results would support my logic (and Carroll’s explanation) that running would be a bad idea. It turns out I was wrong. The simulation—which is different than Win Probability—gave Seattle an 85 percent chance of winning by running and a 77 percent chance by passing. It turns out the added risk of a sack, penalty, or turnover was not worth the other considerations of time and down.
Discussion
Why do you think the simulations for passing and running both give lower results that the Win Probability cited earlier?
Lotto mania
We received the following reference from John White, a longtime Chance News reader, who remembers a fruitful correspondence with Laurie Snell some years ago regarding lottery odds.
- Lottomania: Mega Millions madness
- by John K. White, Counterpunch, 12 February 2015.
This essay laments the never-ending enthusiasm that governments seem to have have for lotteries as revenue generators. John 's historical references range from the 1530 La Lotto de Firenze to Louis XIV to the Irish Sweepstakes. He criticizes modern-day advertising campaigns that entice citizens to play, with tales of imagined winnings and promises that revenues go support various public works. Lottery websites tabulate the frequencies with which various numbers appear in the drawings. Ideally, this would help demonstrate that the lottery is fair; instead, it tends to make players vulnerable to superstitious "hot" and "cold" number betting systems. Perhaps, John concludes, lottery tickets might include printed warnings like those required for cigarettes: “Playing lotteries decreases your chances of saving” or “Player not likely to win in 10,000 lifetimes.”