Sandbox: Difference between revisions
| Line 25: | Line 25: | ||
[http://fortune.com/2018/07/30/alzheimers-biogen-eisai-ban2401/ Why the latest Alzheimer’s drug study has so many people confused]<br> | [http://fortune.com/2018/07/30/alzheimers-biogen-eisai-ban2401/ Why the latest Alzheimer’s drug study has so many people confused]<br> | ||
by Clifton Leaf, ''Fortune'', 30 July 2018 | by Clifton Leaf, ''Fortune'', 30 July 2018 | ||
---- | |||
[https://www.nytimes.com/2018/08/10/opinion/politics/giuliani-trump-chicago-data-crime.html Too Many Politicians Misuse and Abuse Crime Data]<br> | |||
by David Eads, ''New York Times'', 10 August 2018 | |||
==Some math doodles== | ==Some math doodles== | ||
Revision as of 20:15, 10 August 2018
Forsooth
Quotations
“We know that people tend to overestimate the frequency of well-publicized, spectacular events compared with more commonplace ones; this is a well-understood phenomenon in the literature of risk assessment and leads to the truism that when statistics plays folklore, folklore always wins in a rout.”
In progress
More sidewalk tents, but fewer people living in them? The 2018 homeless count's new math
Los Angeles Times
How a 9-year-old boy’s statistic shaped a debate on straws
by Niraj Chokshi, New York Times, 19 July 19 2018
If you say something is “likely,” how likely do people think it is?
by Andrew Mauboussin and Michael J. Mauboussin, Harvard Business Review, 3 July 2018
Words of estimative probability
Why the latest Alzheimer’s drug study has so many people confused
by Clifton Leaf, Fortune, 30 July 2018
Too Many Politicians Misuse and Abuse Crime Data
by David Eads, New York Times, 10 August 2018
Some math doodles
<math>P \left({A_1 \cup A_2}\right) = P\left({A_1}\right) + P\left({A_2}\right) -P \left({A_1 \cap A_2}\right)</math>
<math>P(E) = {n \choose k} p^k (1-p)^{ n-k}</math>
<math>\hat{p}(H|H)</math>
<math>\hat{p}(H|HH)</math>
Accidental insights
My collective understanding of Power Laws would fit beneath the shallow end of the long tail. Curiosity, however, easily fills the fat end. I long have been intrigued by the concept and the surprisingly common appearance of power laws in varied natural, social and organizational dynamics. But, am I just seeing a statistical novelty or is there meaning and utility in Power Law relationships? Here’s a case in point.
While carrying a pair of 10 lb. hand weights one, by chance, slipped from my grasp and fell onto a piece of ceramic tile I had left on the carpeted floor. The fractured tile was inconsequential, meant for the trash.

As I stared, slightly annoyed, at the mess, a favorite maxim of the Greek philosopher, Epictetus, came to mind: “On the occasion of every accident that befalls you, turn to yourself and ask what power you have to put it to use.” Could this array of large and small polygons form a Power Law? With curiosity piqued, I collected all the fragments and measured the area of each piece.
| Piece | Sq. Inches | % of Total |
|---|---|---|
| 1 | 43.25 | 31.9% |
| 2 | 35.25 | 26.0% |
| 3 | 23.25 | 17.2% |
| 4 | 14.10 | 10.4% |
| 5 | 7.10 | 5.2% |
| 6 | 4.70 | 3.5% |
| 7 | 3.60 | 2.7% |
| 8 | 3.03 | 2.2% |
| 9 | 0.66 | 0.5% |
| 10 | 0.61 | 0.5% |
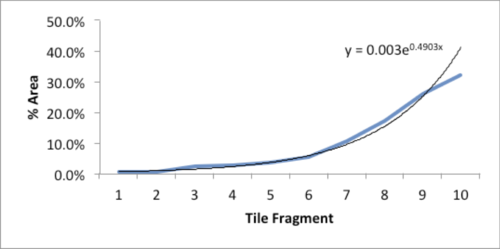
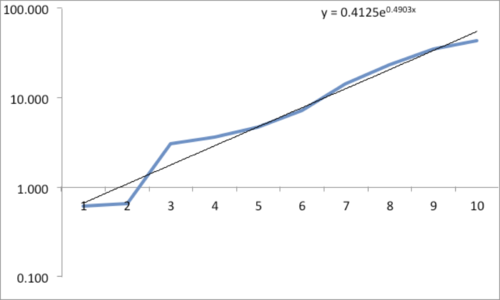
The data and plot look like a Power Law distribution. The first plot is an exponential fit of percent total area. The second plot is same data on a log normal format. Clue: Ok, data fits a straight line. I found myself again in the shallow end of the knowledge curve. Does the data reflect a Power Law or something else, and if it does what does it reflect? What insights can I gain from this accident? Favorite maxims of Epictetus and Pasteur echoed in my head: “On the occasion of every accident that befalls you, remember to turn to yourself and inquire what power you have to turn it to use” and “Chance favors only the prepared mind.”
My “prepared” mind searched for answers, leading me down varied learning paths. Tapping the power of networks, I dropped a note to Chance News editor Bill Peterson. His quick web search surfaced a story from Nature News on research by Hans Herrmann, et. al. Shattered eggs reveal secrets of explosions. As described there, researchers have found power-law relationships for the fragments produced by shattering a pane of glass or breaking a solid object, such as a stone. Seems there is a science underpinning how things break and explode; potentially useful in Forensic reconstructions. Bill also provided a link to a vignette from CRAN describing a maximum likelihood procedure for fitting a Power Law relationship. I am now learning my way through that.
Submitted by William Montante