Sandbox
Forsooth
Quotations
“We know that people tend to overestimate the frequency of well-publicized, spectacular events compared with more commonplace ones; this is a well-understood phenomenon in the literature of risk assessment and leads to the truism that when statistics plays folklore, folklore always wins in a rout.”
Redefining statistical significance
Scholars take aim at false positives in research
by Thomas Gaulkin, UChicagoNews, 1 September 2017
University Chicago economist John List is one of 72 collaborators whose commentary, Redfine statistical significance, was just published in Nature Human Behavior. The subtitle reads, "We propose to change the default P-value threshold for statistical significance from 0.05 to 0.005 for claims of new discoveries."
The natural selection of bad science
It will be much harder to call new findings ‘significant’ if this team gets its way
In progress
Spurious chart, data on N.R.A. spending mislead in gun Debate
by Linda Qiu, New York Times, 3 October 2017
The “500-year” flood, explained: why Houston was so underprepared for Hurricane Harvey
by Dara Lind, Vox, 28 August 2017
The subtitle notes that Hurricane Harvey has produced Houston's third “500-year” flood in the past three years.
Harvey’s test: Businesses struggle with flawed insurance as floods multiply
by Ruth Simon and Cameron McWhirter, Wall Street Journal, 29 August 2017
"Twenty storms causing a billion dollars or more in damage have taken place since 2010, not including Hurricane Harvey, compared with nine billion-dollar floods in the full decade of the 1980s, according to inflation-adjusted estimates from the National Oceanic and Atmospheric Administration."
Brigitte Baldi StatEd It’s time To ditch the concept of ‘100-year floods’
Here's Why Sometimes Correlation Does Actually Imply Causation
The new front in the gerrymandering wars: Democracy vs. math
What Exxon Mobil didn’t say about climate change
by Geoffrey Supran and Naomi Oreskes, New York Times, 22 August 2017
Facebook digital ads figures differ from census data: analyst
Don’t base all your Amazon purchases on the number of reviews a product has
by Corinne Purtill, Quartz, 23 August 2017
The Love of Large Numbers: A Popularity Bias in Consumer Choice
Some math doodles
<math>P \left({A_1 \cup A_2}\right) = P\left({A_1}\right) + P\left({A_2}\right) -P \left({A_1 \cap A_2}\right)</math>
<math>P(E) = {n \choose k} p^k (1-p)^{ n-k}</math>
<math>\hat{p}(H|H)</math>
<math>\hat{p}(H|HH)</math>
Accidental insights
My collective understanding of Power Laws would fit beneath the shallow end of the long tail. Curiosity, however, easily fills the fat end. I long have been intrigued by the concept and the surprisingly common appearance of power laws in varied natural, social and organizational dynamics. But, am I just seeing a statistical novelty or is there meaning and utility in Power Law relationships? Here’s a case in point.
While carrying a pair of 10 lb. hand weights one, by chance, slipped from my grasp and fell onto a piece of ceramic tile I had left on the carpeted floor. The fractured tile was inconsequential, meant for the trash.

As I stared, slightly annoyed, at the mess, a favorite maxim of the Greek philosopher, Epictetus, came to mind: “On the occasion of every accident that befalls you, turn to yourself and ask what power you have to put it to use.” Could this array of large and small polygons form a Power Law? With curiosity piqued, I collected all the fragments and measured the area of each piece.
| Piece | Sq. Inches | % of Total |
|---|---|---|
| 1 | 43.25 | 31.9% |
| 2 | 35.25 | 26.0% |
| 3 | 23.25 | 17.2% |
| 4 | 14.10 | 10.4% |
| 5 | 7.10 | 5.2% |
| 6 | 4.70 | 3.5% |
| 7 | 3.60 | 2.7% |
| 8 | 3.03 | 2.2% |
| 9 | 0.66 | 0.5% |
| 10 | 0.61 | 0.5% |
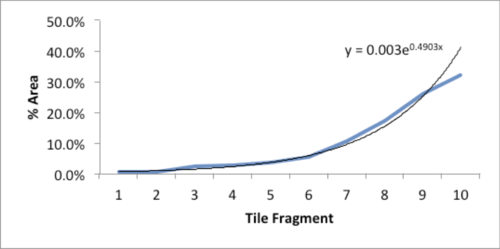
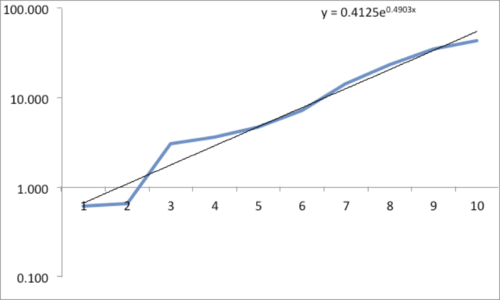
The data and plot look like a Power Law distribution. The first plot is an exponential fit of percent total area. The second plot is same data on a log normal format. Clue: Ok, data fits a straight line. I found myself again in the shallow end of the knowledge curve. Does the data reflect a Power Law or something else, and if it does what does it reflect? What insights can I gain from this accident? Favorite maxims of Epictetus and Pasteur echoed in my head: “On the occasion of every accident that befalls you, remember to turn to yourself and inquire what power you have to turn it to use” and “Chance favors only the prepared mind.”
My “prepared” mind searched for answers, leading me down varied learning paths. Tapping the power of networks, I dropped a note to Chance News editor Bill Peterson. His quick web search surfaced a story from Nature News on research by Hans Herrmann, et. al. Shattered eggs reveal secrets of explosions. As described there, researchers have found power-law relationships for the fragments produced by shattering a pane of glass or breaking a solid object, such as a stone. Seems there is a science underpinning how things break and explode; potentially useful in Forensic reconstructions. Bill also provided a link to a vignette from CRAN describing a maximum likelihood procedure for fitting a Power Law relationship. I am now learning my way through that.
Submitted by William Montante