Chance News 86: Difference between revisions
m (→Quotations) |
m (→Quotations) |
||
| Line 33: | Line 33: | ||
The "inter-ocular traumatic test" is attributed to Joseph Berkson, who also advocated logistic models. | The "inter-ocular traumatic test" is attributed to Joseph Berkson, who also advocated logistic models. | ||
</blockquote> | </blockquote> | ||
Further sleuthing by Bill turned up the 1963 paper, [http://www.stat.cmu.edu/~fienberg/Statistics36-756/Edwards_Lindman1963.pdf Bayesian statistical inference for psychological research], in which Edwards, Lindman and Savage cite a personal communication from Berkson for the test [footnote, p. 217]. | Further sleuthing by Bill J. turned up the 1963 paper, [http://www.stat.cmu.edu/~fienberg/Statistics36-756/Edwards_Lindman1963.pdf Bayesian statistical inference for psychological research], in which Edwards, Lindman and Savage cite a personal communication from Berkson for the test [footnote, p. 217]. | ||
---- | ---- | ||
“Then said Daniel to Melzar …, Prove thy servants … ten days; and let them give us pulse [vegetables] to eat, and water to drink. Then let our countenances be looked upon before thee, and the countenance of the children that eat of the portion of the king’s meat: and as thou seest, deal with thy servants.<br> | “Then said Daniel to Melzar …, Prove thy servants … ten days; and let them give us pulse [vegetables] to eat, and water to drink. Then let our countenances be looked upon before thee, and the countenance of the children that eat of the portion of the king’s meat: and as thou seest, deal with thy servants.<br> | ||
Revision as of 20:14, 16 October 2012
June 12, 2012 to July 18, 2012
Quotations
"Asymptotically we are all dead."
Submitted by Paul Alper
"To err is human, to forgive divine but to include errors in your design is statistical."
Submitted by Bill Peterson
"The only statistical test one ever needs is the IOTT or 'interocular trauma test.' The result just hits one between the eyes. If one needs any more statistical analysis, one should be working harder to control sources of error, or perhaps studying something else entirely."
Krantz is describing how some psychologists view statistical testing. On the same page he describes another viewpoint:
- "Nothing is due to chance. This is the Freudian stance...but fortunately, it has little support among researchers."
Submitted by Paul Alper
Note. Bill Jefferys provided this link to an earlier description of the IOTT (Notes and Quotes. … Rasch Measurement Transactions, 1989, 3:2 p.53):
Rejection of a true null hypothesis at the 0.05 level will occur only one in 20 times. The overwhelming majority of these false rejections will be based on test statistics close to the borderline value. If the null hypothesis is false, the inter-ocular traumatic test ["hit between the eyes"] will often suffice to reject it; calculation will serve only to verify clear intuition." W. Edwards, Harold Lindman, Leonard J. Savage (1962) Bayesian Statistical Inference for Psychological Research. University of Michigan. Institute of Science and Technology.
The "inter-ocular traumatic test" is attributed to Joseph Berkson, who also advocated logistic models.
Further sleuthing by Bill J. turned up the 1963 paper, Bayesian statistical inference for psychological research, in which Edwards, Lindman and Savage cite a personal communication from Berkson for the test [footnote, p. 217].
“Then said Daniel to Melzar …, Prove thy servants … ten days; and let them give us pulse [vegetables] to eat, and water to drink. Then let our countenances be looked upon before thee, and the countenance of the children that eat of the portion of the king’s meat: and as thou seest, deal with thy servants.
“So he consented to them in this matter, and proved them ten days. And at the end of ten days their countenances appeared fairer and fatter in flesh than all the children which did eat the portion of the king’s meat.”
cited by Tim Hartford in Adapt, 2011, p. 132
Submitted by Margaret Cibes
"The problem in social psychology (to reveal my own prejudices about this field) is that interesting experiments are not repeated. The point of doing experiments is to get sexy results which are reported in the popular media. Once such an experiment has been done, there is no point in repeating it."
See further discussion below.
Submitted by Paul Alper
Forsooth
“The survey interviewed 991 Americans online from June 28-30. The precision of the Reuters/Ipsos online polls is measured using a credibility interval. In this case, the poll has a credibility interval of plus or minus 3.6 percentage points.” (emphasis added)
Huffington Post, July 1, 2012
Submitted by Margaret Cibes
“While the study tracked just under 400 babies, the researchers said the results were statistically significant because it relied on weekly questionnaires filled out by parents.”
This was flagged by Gary Schwitzer at HealthNewsReview.org, who commented, "Our reaction: Huh? This sentence makes no sense. Statistical significance is not determined by parents filling out questionnaires."
Submitted by Paul Alper
Gaydar
The science of ‘gaydar’
by Joshua A. Tabak and Vivian Zayas, New York Times, 3 June 2012
The definition of GAYDAR is the "Ability to sense a homosexual" according to internetslang.com.
In their NYT article, Tabak and Zayas write
Should you trust your gaydar in everyday life? Probably not. In our experiments, average gaydar judgment accuracy was only in the 60 percent range. This demonstrates gaydar ability — which is far from judgment proficiency. But is gaydar real? Absolutely.
At PLoS One is their complete research paper where subjects viewed facial photographs of homosexuals and straights; the subjects then had a short time to decide the sexual orientation. In their first experiment, the faces were shown upright only:
Twenty-four University of Washington students (19 women; age range = 18–22 years) participated in exchange for extra course credit. Data from seven additional participants were excluded from analyses due to failure to follow instructions (n = 4) or computer malfunction (n = 3).
In the second experiment, faces were shown upright and upside-down and the subjects had a short time to decide the sexual orientation:
One hundred twenty-nine University of Washington students (92 women; age range = 18–25 years) participated in exchange for extra course credit. Data from 16 additional participants were excluded from analyses due to failure to follow instructions (n = 12) or average reaction times more than 3 SD above the mean (n = 4).
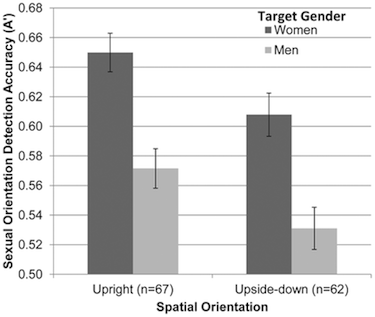
According to the authors, “there are two components of “accuracy”: the hit rate which is “the proportion of gay faces correctly perceived as gay, and the false alarm rate” which is “the proportion of straight faces incorrectly perceived as gay.” The figure reproduced below (full version here) indicates that the accuracy was better when the target gender was women as opposed to men and the accuracy was better when the faces were upright as opposed to upside down. Presumably, random guessing would produce an “accuracy” of about .5.
- Figure 3. Accuracy of detecting sexual orientation from upright and upside-down faces (Experiment 2).
- Mean accuracy (A′) in judging sexual orientation from faces presented for 50 milliseconds as a function of the target’s gender and spatial orientation (upright or upside-down; Experiment 2). Judgments of upright faces are based on both configural and featural processing, whereas judgments of upside-down faces are based only on featural face processing. Error bars represent ±1 SEM.
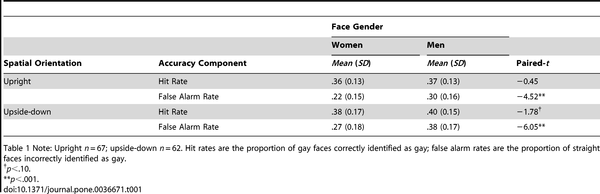
Reproduced below are the detailed results for the second experiment:
- Table 1. Hit and False Alarm Rates for Snap Judgments of Sexual Orientation in Experiment 2.
The author’s conclude with the following statement:
The present research is the first to demonstrate (a) that configural face processing significantly contributes to perception of sexual orientation, and (b) that sexual orientation is inferred more easily from women’s vs. men’s faces. In light of these findings, it is interesting to note the popular desire to learn to read faces like books. Considering how challenging it is to read a book upside-down, it seems that we read faces better than we read books.
Discussion
1. Gaydar "accuracy" seems to be defined in the paper as hit rate / (hit rate + false alarm rate) or, to use terms common in medical tests, positive predictive value = true positive / (true positive + false positive). The paper makes no mention of negative predictive value = true negative / (true negative + false negative). As is illustrated in the Wikipedia article, legitimate medical tests will tolerate a low positive predictive value because a more expensive test exists in the rare case that the disease is actually present; negative predictive values must be high to avoid potentially deadly false optimism. The situation here is somewhat different because the subjects were exposed to an approximately equal number of gays and straights whereas in medical tests, most people in the population do not have the “disease.”
2. Perhaps the analogy with medical testing is inappropriate. That is, an error is an error and no distinction should be made between the two types of errors. Consider the above table for the case of women and upright spatial orientation. The hit rate is .36 and the false alarm rate is .22. If we assume that the 67 subjects viewed 100 gay faces and 100 straight faces, then we obtain the following table for average values:
| Orientation | + | - | Total |
|---|---|---|---|
| Gay | 36 | 64 | 100 |
| Straight | 22 | 78 | 100 |
| Total | 58 | 142 | 200 |
This leads to Prob (success) = (36 + 78)/200 = .57; Prob (error) = (64 +22)/200 = .43 In effect, the model could be hidden tosses of a coin and the subjects, in an ESP fashion, guess heads or tails before the toss. Of course, a Bayesian would then assume a prior distribution and combine that with the results of the study to obtain a posterior probability and avoid any mention of p-value based on .5 as the null.
3. Why might the following be a useful way of assessing gaydar via a modification of the procedure used in the article? Repeat the second experiment with no gays.
4. Why might the following be a useful way of assessing gaydar via a modification of the procedure used in the article? Repeat the second experiment with no straights.
5. In case the reader feels that Discussion #3 and #4 are deceptive, see this Psychwiki which looks at the history of deception in social psychology:
deception can often be seen in the “cover story” for the study, which provides the participant with a justification for the procedures and measures used. The ultimate goal of using deception in research is to ensure that the behaviors or reactions observed in a controlled laboratory setting are as close to those behaviors and reactions that occur outside of the laboratory setting.
Submitted by Paul Alper
Coin experiments
“The Pleasures of Suffering for Science”, The Wall Street Journal, June 8, 2012
This story, about scientists experimenting on themselves, included a reference to a coin-tossing experiment:
Even mathematics offers an example of physical self-sacrifice, through repetitive stress injury. University of Georgia professor Pope R. Hill flipped a coin 100,000 times to prove that heads and tails would come up an approximately equal number of times. The experiment lasted a year. He fell sick but completed the count, though he had to enlist the aid of an assistant near the end.
A Google search for Prof. Hill turned up the following story at the “Weird Science” website:
If you repeatedly flip a coin, the law of probability states that approximately half the time you should get heads and half the time tails. But does this law hold true in practice?
Pope R. Hill, a professor at the University of Georgia during the 1930s, wanted to find out. But he thought coin-flipping was too imprecise a measurement, since any one coin might be imbalanced, causing it to favor heads or tails.
Instead, he filled a can with 200 pennies. Half were dated 1919, half dated 1920. He shook up the can, withdrew a coin, and recorded its date. Then he returned the coin to the can. He repeated this procedure 100,000 times!
Of the 100,000 draws, 50,145 came out 1920. 49,855 came out 1919. Hill concluded that the law of half and half does work out in practice.
Discussion
1. Do you think that drawing a single coin from among 1919 and 1920 coins - even in a perfectly shaken can - would solve the problem of potential imbalance between heads and tails on any single coin toss? Can you think of any possible imbalance in the former case?
2. In the second story, there is a remarkable relationship between Hill’s final counts. What questions, if any, might it raise in your mind about the experiment?
3. Which is the more accurate expectation from a coin-tossing experiment: (a) “heads and tails would come up an approximately equal number of times” (first story) or (b) “approximately half the time you should get heads and half the time tails” (second story)?
Submitted by Margaret Cibes
Note: In the archives of the Chance Newsletter there is a description of some other historical attempts to empirically demonstrate the chance of heads. We read there:
The French naturalist Count Buffon (1707-1788), known to us from the Buffon needle problem, tossed a coin 4040 times with heads coming up 2048 or 50.693 percent of the time. Karl Pearson tossed a coin 24,000 times with head coming up 12,012 or 50.05 percent of the time. While imprisoned by the Germans in the second world war, South African mathematician John Kerrich tossed a coin 10,000 times with heads coming up 5067 or 50.67 percent of the time. You can find his data in the classic text, Statistics, by Freedman, Pisani and Purves.
New presidential poll may be outlier
“Bloomberg Poll Shows Big But Questionable Obama Lead”
Huffington Post, June 20, 2012
A Bloomberg News national poll shows Obama leading his Republican challenger by a “surprisingly large margin of 53 to 40 percent,” instead of the (at most) single-digit margin shown in other recent polls.
While a Bloomberg representative expressed the same surprise as others, she stated that this result is based on a sample with the same demographics as its previous polls and on its usual methodology.
The article’s author states:
The most likely possibility is that this poll simply represents a statistical outlier. Yes, with a 3 percent margin of error, its Obama advantage of 53 to 40 percent is significantly different than the low single-digit lead suggested by the polling averages. However, that margin of error assumes a 95 percent level of confidence, which in simpler language means that one poll estimate in 20 will fall outside the margin of error by chance alone.
See Bloomberg’s report about the poll here.
Submitted by Margaret Cibes
Further discussion from FiveThirtyEight
Outlier polls are no substitute for news
by Nate Silver, FiveThirtyEight blog, New York Times, 20 June 2012
Silver identifies two options for dealing with such a poll, which a number of news sources have describe as an "outlier." One could simply choose to disregard it, or else "include it in some sort of average and then get on with your life." He offers the following wise advice:
My general view...is that you should not throw out data without a good reason. If cherry-picking the two or three data points that you like the most is a sin of the first order, disregarding the two or three data points that you like the least will lead to many of the same problems.
In the case of the Bloomberg poll, because this organization has a good record on accuracy, he has chosen to include it the overall average of polling results that he uses for FiveThirtyEight forecasts.
One of the further adjustments that he makes in his model is described in his later post, Calculating ‘house effects’ of polling firms (22 June 2012). Silver explains that what often is interpreted as movement in public opinion as measured in two different polls may instead be attributable to systematic tendencies of polling organizations to favor either Democratic or Republican candidates. Reproduced below is a chart from the post showing the size and direction of this so-called "house effect" for some major organizations:
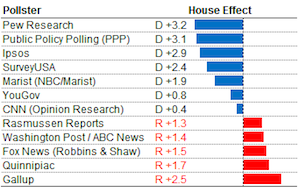
Silver gives the following description for how these estimates are calculated: "The house effect adjustment is calculated by applying a regression analysis that compares the results of different polling firms’ surveys in the same states...The regression analysis makes these comparisons across all combinations of polling firms and states, and comes up with an overall estimate of the house effect as a result." Looking at the table, it is interesting to note that the range of these effects is comparable to the stated margin of sampling error for typical national polls.
Submitted by Bill Peterson
Rock-paper-scissors in Texas elections
“Elections are a Crap Shoot in Texas, Where a Roll of the Dice Can Win”
by Nathan Koppel, The Wall Street Journal, June 19, 2012
The state of Texas permits tied candidates to agree to “settle the matter by a game of chance.” The article describes instances of candidates using a die or a coin to decide an election.
In one case, “leaving nothing to chance, the city attorney drafted a three-page agreement ahead of time detailing how the flip would be conducted.”
However, not any game is permitted:
Tonya Roberts, city secretary for Rice … consulted the Texas secretary of state's office after a city-council race ended last month in a 25-25 tie. She asked whether the race could be settled with a game of "rock, paper, scissors" but was told no. "I guess some people do consider that a game of skill," she said.
For some suggested strategies for winning this game, see “How to Win at Rock, Paper, Scissors” in wikiHow, and/or “To win at rock-paper-scissors, put on a blindfold”, in Discover Magazine.
Discussion
Assume that the use of the rock-paper-scissors game had not been suggested by one of the Rice candidates, who might have been an experienced player. Do you think that a one-time play of this game, between random strangers, could have been considered a game of chance? Why or why not?
Submitted by Margaret Cibes
NSF may stop funding a “soft” science
“Political Scientists Are Lousy Forecasters”
by Jacqueline Stevens, New York Times, June 23, 2012
A Northwestern University political science professor has written an op-ed piece responding to a House-passed amendment that would eliminate NSF grants to political scientists. To date the Senate has not voted on the bill.
She provides several anecdotes about political scientists having made incorrect predictions and states that she is “sympathetic with the [group] behind this amendment.” She feels that:
[T]he government — disproportionately — supports research that is amenable to statistical analyses and models even though everyone knows the clean equations mask messy realities that contrived data sets and assumptions don’t, and can’t, capture. …. It’s an open secret in my discipline: in terms of accurate political predictions …, my colleagues have failed spectacularly and wasted colossal amounts of time and money. …. Many of today’s peer-reviewed studies offer trivial confirmations of the obvious and policy documents filled with egregious, dangerous errors. ….I look forward to seeing what happens to my discipline and politics more generally once we stop mistaking probability studies and statistical significance for knowledge.
Discussion
1. The author makes a number of categorical statements based on anecdotal evidence. Could her conclusions about political science research be an example of the “availability heuristic/fallacy”?
2. Do you think that the problems the author identifies are limited to, or at least more common in, the area of political science than in the other "soft," or even any "hard," sciences? What information would you need in order to confirm/reject your opinion?
(Disclosure: The submitter's spouse is a political scientist, whose Ph.D. program, including stats, was entirely funded by a government act (National Defense Education Act), but who is also skeptical about some social science research.)
Submitted by Margaret Cibes at the suggestion of James Greenwood
Crowdsourcing and its failed prediction on health care law
When the Crowd Isn't Wise
by David Leonhardt, New York Times, July 7, 2012.
Many people were surprised at the U.S. Supreme Court ruling that upheld most aspects of the Affordable Care Act (ACA). That included a prominent source that relied on crowdsoucing. Intrade, an online prediction market. Intrade results indicated that the individual insurance mandate would be ruled unconstitutional. This prediction held steady in spite of some last minute rumors about the Supreme Court decision.
With the rumors swirling, I began to check the odds at Intrade, the online prediction market where people can bet on real-world events, several times a day. The odds had barely budged. They continued to show about a 75 percent chance that the law’s so-called mandate would be ruled unconstitutional, right up until the morning it was ruled constitutional.
The concept of crowdsourcing has been discussed on Chance News before. The basic idea is that individual experts have systematic biases, but these biases cancel out when averaged over a large number of people.
Crowdsourcing does have some notable successes, but it isn't perfect.
For one thing, many of the betting pools on Intrade and Betfair attract relatively few traders, in part because using them legally is cumbersome. (No, I do not know from experience.) The thinness of these markets can cause them to adjust too slowly to new information.
And there is this: If the circle of people who possess information is small enough — as with the selection of a vice president or pope or, arguably, a decision by the Supreme Court — the crowds may not have much wisdom to impart. “There is a class of markets that I think are basically pointless,” says Justin Wolfers, an economist whose research on prediction markets, much of it with Eric Zitzewitz of Dartmouth, has made him mostly a fan of them. “There is no widely available public information.”
So, should you return to the individual expert for prediction? Maybe not.
Mutual fund managers, as a class, lose their clients’ money because they do not outperform the market and charge fees for their mediocrity. Sports pundits have a dismal record of predicting games relative to the Las Vegas odds, which are just another market price. As imperfect as prediction markets are in forecasting elections, they have at least as good a recent record as polls. Or consider the housing bubble: both the market and most experts missed it.
Mr. Leonhardt offers a middle path.
The answer, I think, is to take the best of what both experts and markets have to offer, realizing that the combination of the two offers a better window onto the future than either alone. Markets are at their best when they can synthesize large amounts of disparate information, as on an election night. Experts are most useful when a system exists to identify the most truly knowledgeable — a system that often resembles a market.
This last sentence introduces the thought that you use crowdsourcing to find the best experts. Social media like Twitter allows people an interesting way to identify experts who are truly experts.
Think for a moment about what a Twitter feed is: it’s a personalized market of experts (and friends), in which you can build your own focus group and listen to its collective analysis about the past, present and future. An RSS feed, in which you choose blogs to read, works similarly. You make decisions about which experts are worthy of your attention, based both on your own judgments about them and on other experts’ judgments.
Their predictions now face a market discipline that did not always exist before the Internet came along. “Experts exist,” as Mr. Wolfers says, “but they’re not necessarily the same as the guys on TV.”
Questions
1. How bad did Intrade really perform on the Supreme Court decision on ACA? How large a probability does a system like Intrade have to place on a bad prediction to cause you to lose faith in it?
2. What are some of the potential problems with identifying experts by the number of retweets that they get in Twitter?
Submitted by Steve Simon
Dicey procedure
The novel Something Missing [1] (by Matthew Dicks, 2009) contained the following sentence:
In every other client’s home, Martin had at least three means of egress and would use each on a random basis (rolling a ten-sided die that he kept in his pocket to determine each day’s exit ….).
Note that the book’s title might be applied to this quotation alone!
Discussion
Suppose that Martin tossed a die exactly once, to decide which of three equally probable exits to use. Assume that all dice referred to below have equally weighted faces.
- Obviously, the most common die shapes are the platonic solids (4, 6, 8, 12, 20 faces). Which of these shapes, if any, could he have used? If so, how?
- There is at least one die shape with 10 faces: “A pentagonal trapezohedron … has ten faces … which are congruent kites.”[2] Can you think of a way to use two pyramids to make a die with 10 congruent triangular faces?
- If you were not restricted to exactly one toss, in what way, if any, could you use one of these 10-faced dice to make this decision?
- If you were not restricted to equally weighted, or congruent polygonal, faces, could you design a 10-faced die that could be used to make this decision in exactly one toss?
For a discussion of dice in general – odd numbers of sides, curved sides, etc. - see Wikipedia’s ”Dice” article.
Submitted by Margaret Cibes
Myth resurfaces
“A Blizzard of Babies From October Storm? Probably Not”
by William Weir, The Hartford Courant, July 12, 2012
A local CT hospital is expecting an increase in July and August births as a result of a freaky, disastrous October 2012 snow storm in New England.
The idea that a baby boom would result from a calamitous event has become lore that has persisted with the help of the romantics of the world. It began with a series of New York Times articles in 1966 reporting that city hospitals saw a spike in births nine months after a massive blackout in the Northeast. What a great story, people thought — and the notion that blackouts should beget amorousness grew into conventional wisdom. …. "It is kind of an urban myth," said [a D.C. demographer]. "We've never been able to show it specifically. I hate to say that — it's a very popular idea."
See link to Richard Udry’s “The Effect of the Great Blackout of 1965 on Births in New York City”, Demography, August 1970. Data is included.
Submitted by Margaret Cibes
Statistics and the Higgs boson
Physicists find elusive particle seen as key to universe
by Dennis Overbye, New York Times, 4 July 2012
In the article, we read
The December signal was no fluke, the scientists said Wednesday. The new particle has a mass of about 125.3 billion electron volts, as measured by the CMS group, and 126 billion according to Atlas. Both groups said that the likelihood that their signal was a result of a chance fluctuation was less than one chance in 3.5 million, “five sigma,” which is the gold standard in physics for a discovery.
This is a common misstatement of the meaning of a P-value. The one-in-3.5 million is the probability that an signal as large as the scientists observed (or larger) would occur by chance variation assuming the null hypothesis is true (i.e., there is no real effect). It is not the probability that the observed signal was due to chance variation.
On another note, in his essay, A blip that speaks of our place in the universe (New York Times, 9 July 2012), Lawrence Krauss writes about the staggering amount of data collected for these experiments:
Every second at the Large Hadron Collider, enough data is generated to fill more than 1,000 one-terabyte hard drives — more than the information in all the world’s libraries. The logistics of filtering and analyzing the data to find the Higgs particle peeking out under a mountain of noise, not to mention running the most complex machine humans have ever built, is itself a triumph of technology and computational wizardry of unprecedented magnitude.
See also The role of statistics in the Higgs Boson discovery from RBloggers for a good description of the research for non-physics-specialists.
Discussion
The P-value problem was noted on a number of blog posts, including this one, which is flagged with the warning "For statistical pedants only." Are we being too sentitive? That is, do you think the confusion of P(data | H0) with P(H0 | data) is a pedantic matter, or an important distinction for lay communicators to understand?
Submitted by Bill Peterson
How to prove anything with statistics
Statisticians can prove almost anything, a new study finds
by Joseph Brean, National Post (Toronto, Canada), 20 November 2011
This article describes an academic paper, False-positive psychology: Undisclosed flexibility in data collection and analysis allows presenting anything as significant, by Joseph Simmons, Leif Nelson and Uri Simonsohn in Psychological Science, 2011. As described here, the authors
...wanted to prove the hypothesis that listening to children's music makes you older. (Not makes you *feel* older, but actually makes your date of birth earlier.) Obviously, that hypothesis is false.
Still, the authors managed to find statistical significance. It turned out that subjects who were randomly selected to listen to "When I'm Sixty Four" had an average (adjusted) age of 20.1 years, but those who listened to the children's song "Kalimba" had an adjusted age of 21.5 years. That was significant at p=.04.
How? Well, they gave the subjects three songs to listen to, but only put two in the regression. They asked the subjects 12 questions, but used only one in the regression. And, they kept testing subjects 10 at a time until they got significance, then stopped.
In other words, they tried a large number of permutations, but only reported the one that led to statistical significance.
Further comments can be found here, where one contributor posted the following very appropriate cartoon from XKCD (full-sized original here).
Regarding Simonsohn--one of the co-authors on the Psychological Science paper--his blockbuster paper is yet to come out ("Finding Fake Data: Four True Stories, Some Stats and a Call for Journals to Post All Data") but already he has fingered a researcher in Holland, Dirk Smeesters, who has resigned over messing with the data to get a p-value less than .05. Simonsohn's method is technical, but according to Prof. Gill of Leiden University
Simonsohn's idea (according to Erasmus-CWI) is that if extreme data has been removed in an attempt to decrease variance and hence boost significance, the variance of sample averages will decrease. Now researchers in social pyschology typically report averages, sample variances, and sample sizes of subgroups of their respondents, where the groups are defined partly by an intervention (treatment/control) and partly by covariates (age, sex, education ...). So if some of the covariates can be assumed to have no effect at all, we effectively have replications: i.e., we see group averages, sample variances, and sample sizes, of a number of groups whose true means can be assumed to be equal. Simonsohn's test statistic for testing the null-hypothesis of honesty versus the alternative of dishonesty is the sample variance of the reported averages of groups whose mean can be assumed to be equal. The null distribution of this statistic is estimated by a simulation experiment, by which I suppose is meant a parametric bootstrap. Presumably this means a background assumption of normal distributions. In the bootstrap experiment, we pretend that the reported group variances are population values, we pretend that the actual sample sizes are the reported sample sizes, and we play being an honest researcher who takes normally distributed samples of these sizes and variances, with the same mean.
Details on the Smeesters case can be found in the report from the Committee on Scientific Integrity at Erasmus University. We read there (p. 3) the following description of Simonsohn's method:
The analysis of Simonsohn is based on the assumption that given the standard deviations of the experimental conditions reported in an article, there should be sufficient variations in reported averages of groups of conditions that are assumed to stem from the same population. If multiple samples are drawn (one sample per condition) then the averages of these samples should be automatically sufficiently dispersed. Simonsohn argues that if the averages of the groups vary too little, this is an indication of problems with the data.
(Further elaboration appears on p. 5 of the report.)
Gill has this to say:
My overall opinion is that Simonsohn has probably found a useful investigative tool. In this case it appears to have been used by the Erasmus committee on scientific integrity like a medieval instrument of torture: the accused is forced to confess by being subjected to an onslaught of vicious p-values which he does not understand. Now, in this case, the accused did have a lot to confess to: all traces of the original data were lost (both original paper, and later computer files), none of his co-authors had seen the data, all the analyses were done by himself alone without assistance. The report of Erasmus-CWI hints at even worse deeds. However, what if Smeesters had been an honest researcher?
Submitted by Paul Alper