Chance News 84
April 1, 2012 to April 30, 2012
Quotations
"There's a saying in the San Francisco Bay Area: There are lies, damned lies, and next bus."
Submitted by Jerry Grossman
"Skepticism enjoins scientists — in fact all of us — to suspend belief until strong evidence is forthcoming, but this tentativeness is no match for the certainty of ideologues and seems to suggest to many the absurd idea that all opinions are equally valid. ...What else explains the seemingly equal weight accorded to the statements of entertainers and biological researchers on childhood vaccines?..."
Submitted by Bill Peterson
From Significance magazine, February 2012:
“Diaconis and Mosteller … introduced an adage that they called the law of truly large numbers: with a large enough sample, almost anything outrageous will happen.”
“[After a drug trial] no one in the world wants to know what the chance is that, for this experimental group, A was better than B …. We know exactly what the chance is, because the event has already happened. …. The probability that A was better, given this evidence, is either 1 or 0. …. What the drug company actually wants to know is, given the evidence from the trial, and possibly given other evidence about the two drugs, what are the chances that a greater proportion of future patients will get better if they take A instead of B? …. [After a hypothesis test] the civilian assumes that his original question has been answered and that the probability that A is better is high. But he should not believe this, because of course it might not be true. The p-value can be small, as small as you like, and the probability that A is better could still be low.”
Submitted by Margaret Cibes
"If you want to show that things are better, study the mortality rate, not the survival rate."
Carroll is criticizing this article comparing cost-effectiveness of cancer treatments in the US and Europe. (The notion that screening saves lives because it improves the metric known as the 5-year survival rate is a difficult one to counter in the mind of the lay public.)
Submitted by Paul Alper
"Delbanco’s is not an argument for, but a display of, the value of a liberal arts education.
"The display comes in two forms. First there is the felicity of the author’s prose. Mirabile dictu, there are no charts and few statistics."
Fish is reviewing Delbanco's book, College: What it Was, Is, and Should Be
Submitted by Paul Alper
“It is a capital mistake to theorize before you have all the evidence. It biases the judgment.”
“It is a capital mistake to theorize before one has data. Insensibly one begins to twist facts to suit theories, instead of theories to suit facts.”
“The country needs and, unless I mistake its temper, the country demands bold, persistent experimentation. It is common sense to take a method and try it: If it fails, admit it frankly and try another. But above all, try something. The millions who are in want will not stand by silently forever while the things to satisfy their needs are within easy reach.”
Submitted by Margaret Cibes (citations from The Upside of Irrationality, 2010)
“As I see it, the economics profession went astray because economists, as a group, mistook beauty, clad in impressive-looking mathematics, for truth.”
Submitted by Margaret Cibes at the suggestion of Jim Greenwood
Forsooth
“Let's start with T. Rowe Price's U.S. stock fund lineup. I have plugged in 15 of its largest actively managed U.S. equity funds. Let's start at the top with T. Rowe Price Blue Chip Growth. [Note] that T. Rowe Price Growth Stock is a tight fit with a 1.00 correlation--the highest it can get. So, we know that owning those two large-growth funds is rather redundant. [Note] that Small-Cap Value has the lowest correlation at 0.91--thus, it's a good choice for diversification purposes.”
Submitted by Margaret Cibes
“This past week, Obama sports a 53-44 fav[orable] / unfav[orable] rating among women, but 43-54 among men. That's a whopping 20-point gender gap. .... In 2008, President Barack Obama won women 56-43, while narrowly edging out John McCain among men 49-48. That 12-point gender gap appeared massive at the time, but it appears that we're headed toward an even bigger margin in 2012.”
Submitted by Margaret Cibes
From Significance magazine, February 2012:
“It is ridiculous to believe that the legal profession has to get involved with the complex parts of statistics. The statistics of gambling uses the frequency approach to statistics, and that is straightforward. The reasoning involved with Bayes is more complex and we cannot expect juries to accept it.”
“Strangely, DNA experts are required to give probabilities for their evidence of matching; fingerprint expert[s] are forbidden to.”
“We cannot increase the probability of winning a [lottery] prize as this is fixed. However, we can increase the amount we can expect to win if we do strike [it] lucky …. [C]hoosing popular combinations of numbers decreases the expected value of your ticket as you have a higher probability of having to share your prize if you win. …. [W]hen you select your numbers, you may as well try to choose a less popular combination that might increase your expected value. Unfortunately, it is not possible to determine what exactly the unpopular combinations are: there is not enough data.”
Submitted by Margaret Cibes
Don't Worry, Be Happy
In their new heart-health book "Heart 411," Cleveland Clinic doctors Marc Gillinov and Steven Nissen describe a study by Wayne State University researchers who rated the smiles of 230 baseball players who played before 1950 based on pictures in the Baseball Register. Then they looked to see how long the players lived on average: No smile, age 73; partial smile, 75. Those with a full smile made it to 80.
in: The guide to beating a heart attack, Wall Street Journal, 16 April 2012
Submitted by Paul Alper
"The New England Common Assessment Program (NECAP) is probably one the most challenging. The NY Regents might be a little bit more challenging; Massachusetts, the MCAS, may also be. But [the NECAP] is in the top 2 or 3% of the most challenging state assessments."
in: Vermont evaluating how to improve science and math education, VPR "Vermont Edition", 15 February 2012 (at ~15:03 in the audio.)
Submitted by Jeanne Albert
Chocolate hype
“Association Between More Frequent Chocolate Consumption and Lower Body Mass Index”
Archives of Internal Medicine, March 26, 2012
This report (full text not yet available online) was published as a “research letter.” It involved about 1000 Southern Californians, who were surveyed about their eating and drinking habits and whose BMIs were computed. Funded by the National Institutes of Health, the study found that, among this group, people who ate chocolate more frequently had lower BMIs than less frequent chocolate eaters. The authors, in the “research letter” at least, apparently did not claim any cause-and-effect result and indicated that a controlled study would be needed before jumping to any such conclusion.
The Knight Science Journalism Tracker (subtitled “Peer review within science journalism”) presented a nice critique of press accounts of the “research letter” in “Eat Chocolate. Lose Weight. Yeah, right.”.
Before I became aware of the Knight project, I had tracked down a number of press accounts of the study and was encouraged to find it appropriately described in the articles, if not in the headlines, as non-definitive. (This is not to say that all reports were accurate or complete with respect to other aspects of the study.) Comparing media reports to original study reports might be a good exercise for a stats class, when a similarly enticing topic presents itself in the news, and when the original study report, or even an abstract, is available for comparison.
(a) The New York Times[3]: “Dietary studies can be unreliable, ... and it is difficult to pinpoint cause and effect.”
(b) BBC News[4]: “But the findings only suggest a link - not proof that one factor causes the other.”
(c) TODAY [5]: “The researchers only found an association, not a direct cause-effect link.”
(d) The Times of India[6]: “[T]he reasons behind this link between chocolate consumption and weight loss remain unclear.”
(e) Reuters[7]: “Researchers said the findings … don't prove that adding a candy bar to your daily diet will help you shed pounds.”
(f) Poughkeepsie Journal[8]: “The study is limited. It was observational, ... rather than a controlled trial ....”
(g) The Wall Street Journal[9]: “[B]efore people hoping to lose weight indulge in an extra scoop of chocolate fudge swirl, the researchers caution that the study doesn't prove a link between frequent chocolate munching and weight loss…..”
Discussion
1. According to Knight, the original purpose of the project was to study “non-cardiac effects on statin drugs,” not chocolate consumption. Should this information have been reported in the articles? Why or why not?
2. Do you think that the size of the chocolate-consuming group was the same as the size of the entire group of respondents? Why would you want to know the “sample” size behind the chocolate results?
3. How would you monitor a controlled study involving a group of people who were instructed to eat chocolate occasionally and another group who were instructed to eat it more frequently?
Submitted by Margaret Cibes
"Hangman" and conditional probability
A better strategy for hangman
by Nick Berry, lifehacker blog, 5 April 2012
If we order the 26 letters by their frequency of occurrence in English, we get:
But does it follow that this is the right order for guessing your first letter in a game of Hangman? A better strategy, Berry argues, is to condition on the length of the word, information that we have at the start of the game. He develops the following table:
| Number of letters | Optimal calling order |
|---|---|
| 1 | A I |
| 2 | A O E I U M B H |
| 3 | A E O I U Y H B C K |
| 4 | A E O I U Y S B F |
| 5 | S E A O I U Y H |
| 6 | E A I O U S Y |
| 7 | E I A O U S |
| 8 | E I A O U |
| 9 | E I A O U |
| 10 | E I A O U |
| 11 | E I A O D |
| 12 | E I A O F |
| 13 | I E O A |
| 14 | I E O |
| 15 | I E A |
| 16 | I E H |
| 17 | I E R |
| 18 | I E A |
| 19 | I E A |
| 20 | I E |
He has some interesting conclusions based on the above conditional probabilities:
- The most challenging (least deterministically obvious) words to guess are three letter words. It can take up to ten guesses before getting a letter on the board!
- With fewer than three letters, it gets easier (there are fewer possible words), and with more than three letters it becomes less likely there will be any words that you cannot find a letter for quickly.
- For five letter words, the best first guess is the letter S. This is the only time a consonant is the most likely first guess letter.
- For four letter words, the first non-vowel guess is an S, followed by B and then F (remember, these are only called if all preceding letters have failed to hit).
- No row contains more than ten guesses, and since a Hangman game takes eleven fails to lose, it is impossible to come up with any English letter word that will fail at Hangman without a single letter appearing on the board (assuming the optimal search strategy above is followed).
- A should only be your first guess if the word length is four or fewer letters. If five letters, go for S first. Between six and twelve letters try E and above that you should call I.
How will this work in practice? Berry notes that "Battle plans are excellent up until the first shot is fired!" Indeed, as Andrew Gelman point out on his blog post, Hangman tips (4 April 2012), if if you knew your opponent was guessing according to these probabilities, you could counter by adjusting your word selections to shift the distribution.
Discussion
1. The sequence
- ETAOIN SHRDLU CMFWYP VBGKQJ XZ
comes from conceptually thinking of a very large bucket which contains all the words in the English language used in a very large book so that common words such as "and," '"or," "but," "down," "I," "me," "birth" and so on appear very frequently; words such as 'hyperventilate" or "colonoscopy" appear less frequently. However, if one thinks of a large bucket which contains all the words in the English language but each word appears only once, then the frequency of occurrence according to Berry is
- ESIARN TOLCDU PMGHBY FVKWZX QJ
Now, if you are told the specific length of a word, we can ignore the words of different length in the very large bucket and this leads to the above table.
2. The sequence
- ETAOIN SHRDLU
is beloved by the cognicenti because of its connection to the printing trade.
Submitted by Paul Alper
Show-and-tell opportunities
Significance, February 2012
Timandra Harkness is a writer and comedian, who is currently on tour in the UK and Australia with her show, “Your Days Are Numbered: the maths of death”. She notes that she’s the “only comedian currently touring the UK who has an article in [a] Journal of the Royal Statistical Society.” The article, “Seduced by stats?”, appears in the February 2012 issue of Significance, a joint production of RSS and ASA.
A Cambridge University professor has created a website, Cambridge Coincidences Collection, where visitors can record and/or read stories about coincidences which they have experienced. He expects to analyze the possible scientific explanations for them and/or the mathematical chances of their occurrence.
Submitted by Margaret Cibes
Red meat and mortality risk
Risks: More red meat, more mortality
by Nicholas Bakalar, New York Times, 12 March 2012
The risk numbers
by Carl Bialik, Wall Street Journal, Numbers Guy blog, 23 March 2012
By now we are all used to hearing that we should eat less red meat. A new study published in the Archives of Internal Medicine (abstract available here) finds that consuming red meat is associated with mortality risk from cancer and heart disease. As described in the NYT article
People who ate more red meat were less physically active and more likely to smoke and had a higher body mass index, researchers found. Still, after controlling for those and other variables, they found that each daily increase of three ounces of red meat was associated with a 12 percent greater risk of dying over all, including a 16 percent greater risk of cardiovascular death and a 10 percent greater risk of cancer death.
In his Numbers Guy post, Carl Bialik calls for a closer examination of "12 percent greater risk" figure, noting that it corresponds to a relative risk, without providing information about absolute risk. He explains that people tend to overreact to information presented in this way. He references the British pharmaceutical industry’s Code of Practice, where, in a section entitled "Misleading Information, Claims and Comparisons" (p. 16), we read:
Reference to absolute risk and relative risk. Referring only to relative risk, especially with regard to risk reduction, can make a medicine appear more effective than it actually is. In order to assess the clinical impact of an outcome, the reader also needs to know the absolute risk involved. In that regard relative risk should never be referred to without also referring to the absolute risk. Absolute risk can be referred to in isolation.
In this YouTube video, Gerd Gigerenzer describes a famous example of the consequences of not understanding the distinction between relative and absolute risk. In 1995, a British study found a 100 percent increase risk of thrombosis for women using third-generation oral contraceptive pills. Widespread media reporting of this figure resulted in public alarm, and many women stopped using the pill. In the year following the report, there were some 13,000 additional abortions in the UK, reversing what had been a downward trend. However, Gigerenzer explains, what the studies actually found was that for every 7000 women who took the pill of the second-generation pills, 1 suffered a thrombosis, compared to 2 per 7000 women who took the third-generation pill. So the relative risk did indeed increase by 100%, but the absolute risk had increased only by 1 in 7000.
Discussion
Of course, we all have a 100% overall chance of dying eventually. So what does the NYT mean by "each daily increase of three ounces of red meat was associated with a 12 percent greater risk of dying over all"?
Submitted by Bill Peterson
The Supreme spittoons
Former Oklahoma AG shares insight into U.S. Supreme Court
by Dan Bewley, News On 6 (Tulsa, OK), 28 March 2012
This backgrounder piece on the experience of arguing before the Supreme Court concludes with the following:
Two other Supreme Court traditions that are interesting, attorneys who argue before the Supreme Court are given a white goose-quill pen to take home as a souvenir.
And just below the bench that the justices sit at, are ceramic spittoons as a remnant of the court's early history, only now they're used as waste baskets.
Regarding the spittoons, Paul Alper wrote to point out the irony in light of the famous statistical controversies surrounding tobacco products!
Debugging your baby
“The Data-Driven Parent”
by Mya Frazier, The Atlantic, May 2012
The subtitle of this one-page article is “Will statistical analytics make for healthier, happier babies—or more-anxious adults?”
There are now many apps – Baby Connect, Total Baby, Baby Log, iBabyLog, Evoz, etc. – that collect data that parents enter, with respect to gazillions of variables, about their children, from birth to who-knows-what age. Apparently these baby-data apps are a “substitute for handwritten diaper-changing … logs.”
Since Baby Connect launched, in 2009, … 100,000 ... users have logged 47 million “events,” including 10 million diaper changes ….
These apps are purported to be “making parenthood a more quantifiable, science-based endeavor.” In the near future, it is claimed, parents will be able to gauge the “normality” of a child through electronic monitoring and a Wi-Fi network. One parent states that this will be a way “to debug your baby for problems.”
(I don't know whether to laugh or cry.)
Submitted by Margaret Cibes
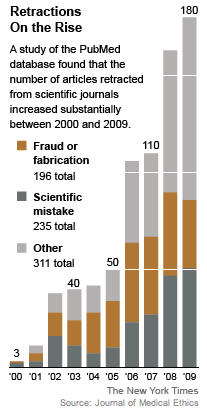
Retractions
A sharp rise in retractions prompts calls for reform
By Carl Simmer, New York Times, 16 April 2012
We read that: "In October 2011, for example, the journal Nature reported that published retractions had increased tenfold over the past decade, while the number of published papers had increased by just 44 percent. In 2010 The Journal of Medical Ethics published a study finding the new raft of recent retractions was a mix of misconduct and honest scientific mistakes." Here is the graphic that accompanies the article
The article gives the following analysis of why the phenomenon "Retractions on the Rise" is happening:
Several factors are at play here, scientists say. One may be that because journals are now online, bad papers are simply reaching a wider audience, making it more likely that errors will be spotted. 'You can sit at your laptop and pull a lot of different papers together,' Dr. Fang said.
But other forces are more pernicious. To survive professionally, scientists feel the need to publish as many papers as possible, and to get them into high-profile journals. And sometimes they cut corners or even commit misconduct to get there.
The article also references the Retraction Watch blog, which was launched in 2010 to keep track of retractions.
Discussion Questions
1. Comment on the presentation in the graphic, particularly in regard to the relative contributions of the three categories.
2. Another factor at play, related to the comment in the first paragraph but not actually treated here, is rising number of journals now being published. How would you incorporate this into the analysis?
Submitted by Paul Alper
Genetically nice
The Holy Grail of genetics is to find the single gene which is responsible for an affliction such as cancer or for some positive attribute such as intelligence. According to MedicineNet.com, "There are thousands of single-gene diseases including achondroplasia, cystic fibrosis, hemophilia, Huntington disease, muscular dystrophy, and sickle cell disease."
Far more elusive is finding a single gene which determines an attribute such as IQ, cooking ability, or musical talent. Or, the very human trait of being “nice.” So, when some connection between nice and a gene is alleged, the lay press gets breathlessly excited:
- From HealthDay News (philly.com, 11 April 2012):
Being nice may be in your genes. That's according to a new study that found that genes are at least part of the reason why some people are kind and generous.
- From the Minneapolis Star Tribune (19 April)
If the researchers behind a recent report in Psychological Science are correct, Minnesota Nice isn't a result of our climate, the copious amount of fried food we consume at the State Fair or the fact that each summer we lead the nation in per capita trips "up north" to "the lake.” It's in our genes.
- From the Times of India (12 April):
Ever wondered why some people are nice and generous while others behave badly? It's because their genes may have nudged them towards developing different personalities, scientists say.
- From CBS News (12 April):
Being a nice person isn’t just because of how your mother raised you: It might be coded into your genes.
A new study, out in the April issue of Psychological Science, shows that people who have certain types of oxytocin and vasopressin receptor genes were more likely to be generous when coupled with that person's outlook on the world.
For the study, [Prof. M.J.] Poulin's team administered an online survey about an individual's attitude toward civic duty, other people, charitable activities, and the world at large. Then saliva samples were taken from 711 subjects to see what version of the oxytocin and vasopressin receptor genes they had.
The study revealed that the genes - coupled with how positive the person viewed the world - tended to relate to nice behavior in participants.
Interestingly enough, those that thought the world was a cruel place but had the right receptor genes to be kind tended to still be generous.
Here is a citation for the study in question: M. J. Poulin, E. A. Holman, A. Buffone, The neurogenetics of nice: Receptor genes for oxytocin and vasopressin interact with threat to predict prosocial behavior, Psychological Science, 2012.
Discussion
1. Because Poulin’s data is both voluntary and observational, he was asked by Chance News if we aren’t still a long way from a niceness gene. His reply was, “That's precisely what I've said to any journalist who will listen. Many of them don't.” Why were the journalists not listening?
2. What are the possible weaknesses of a voluntary, observational data set?
3. The original survey of attitudes was collected several months after September 11, 2001. Additional surveys of attitudes were collected in 2002, 2003, and 2004. The DNA saliva samples were collected in 2008. What problems might this time lapse cause?
4. The CBS News version refers to 711 subjects. The regressions have sample sizes of only 264 and 283 for the dependent variables “engagement in charitable activities” and “commitment to civic duty,” respectively. Poulin says, “I tried to be as transparent about the subsamples as possible in the paper. Press reports do a less-good job of paying attention to these distinctions.” Speculate as to why there is a “less-good job of paying attention to these distinctions.”
Submitted by Paul Alper
The new normal
A tale of two winters
by Matt Sutkoski, Burlington [VT] Free Press, 24 March 2012
A year ago, Vermont was emerging from a cold, snowy winter; this year it feels like winter never quite arrived. According to the article:
As of March 16, this winter [2011-12] had 37.7 inches of snow, compared to a normal of 69.2 and last year’s total of 125.3, again, as of March 16.
The mean temperature this winter (December 1 through February 29) was 27.8 degrees, compared to a normal of 22.0 and last winter’s [2010-11] average temperature of 20.9."
We have all heard weather reports make reference to "normal" precipitation or temperature levels in weather forecasts. But what does "normal" actually mean? As Sutkowski explains, last year normal referred to a 30-year average for the period 1970-2000, whereas this year it refers to 1980-2010. One curious consequence of the switch is that Vermont temperatures in 2010-2011 were close to "normal" in terms of 1970-2000 data, but colder than average for 1980-2010. The National Oceanic and Atmospheric Administration has a web page entitled NOAA 1981-2010 Climate Normals, which provides more details of how the the figures are maintained and updated.
Update: after Sutkowski's article appeared, Vermont, along with much of the eastern half of the country, experienced a week of record warmth. Here is a graphic from the NOAA summary report for the month of March.
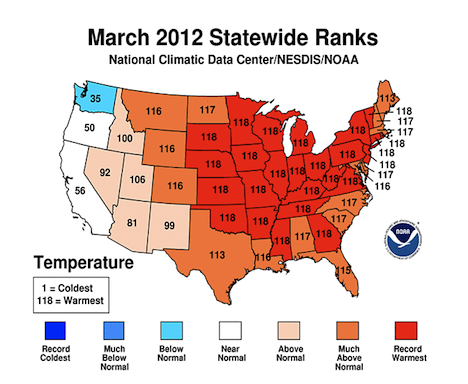
The mysterious numbers shown on the states--they are certainly not temperatures!-- drew commentary from Kaiser Fung in a JunkCharts post entitled The importance of explaining your chart: the case of the red 118. After some sleuthing, Fung found this explanation of NOAA's Climatological Rankings
As a year is added to the inventory, the length of record increases. In 2010, NCDC had 116 years of records, thus the number 116 would represent the warmest or wettest rank; the number 1 would represent the coolest or driest rank. If a state has rank of 110, then it would be the seventh warmest or wettest on record for that time period. If a state rank has a value of 7, then that state ranked seventh out of 116 years, or seventh coolest or driest.
Thus, for much of the east, 2012 saw the warmest March in 118 years of records.
Submitted by Bill Peterson
Honesty
Time to be honest: A simple experiment suggests a way to encourage truthfulness
Economist, 31 March 2012
The article describes an experiment designed to compare people's tendency to lie (in their own favor) about a die roll when asked to respond immediately versus when they have time to reflect. There were actually two versions of the experiment. In the first, the researchers
...gave each of 76 volunteers a six-sided die and a cup. Participants were told that a number of them, chosen at random, would earn ten shekels (about $2.50) for each pip of the numeral they rolled on the die. They were then instructed to shake their cups, check the outcome of the rolled die and remember this roll. Next, they were asked to roll the die two more times, to satisfy themselves that it was not loaded, and, that done, to enter the result of the first roll on a computer terminal. Half of the participants were told to complete this procedure within 20 seconds while the others were given no time limit.
The mean roll reported by those required to respond within 20 seconds was 4.6, compared to 3.9 for those with no time limit. Noting that both of these are above the expected mean of 3.5, the article concludes that "both groups lied."
In the second version,
[a] different bunch of volunteers were asked to roll the die just once. Again, half were put under time pressure and, since there were no additional rolls to make, the restriction was changed from 20 seconds to eight. The others were allowed to consider the matter for as long as they wished.
This time, the mean for the timed group was 4.4, compared with 3.4 for the untimed group. The article reports that the second group was now reporting honestly.
The research article is: Shalvi, S., Eldar, O. & Bereby-Meyer, Y., Honesty requires time (and lack of justifications), to appear in Psychological Science. A pre-publication version is available at Dr. Shalvi's home page.
Discussion
1. Why do you think participants were told that only a random subset of them would receive payment for their rolls?
2. For the first version, the assertion that "both groups lied" presumably means that the observed mean of 3.9 is significantly larger than the theoretical mean of 3.5. How would you assess this? What do you need to assume?
3. Perhaps, when given three rolls, participants were tempted to report the largest roll rather than the first. Is there any evidence for this? Find the expected maximum for 3 rolls of a die and compare with the results from the first version of the experiment.
Submitted by Bill Peterson