Chance News 8
Oct 15 to Oct 30
Quotation
One more fagot of these adamantine bandages, is, the new science of Statistics. It is a rule, that the most casual and extraordinary events -- if the basis of population is broad enough -- become matter of fixed calculation. It would not be safe to say when a captain like Bonaparte, a singer like Jenny Lind, or a navigator like Bowditch, would be born in Boston: but, on a population of twenty or two hundred millions, something like accuracy may be had. Ralph Waldo Emerson Fate
Forsooth
Here's another Forsooth from the October issue of RSS News.
Your'e more likely to die in a fire in Strathclyde than anywhere else in the country
11 May 2005
The Poisson Distribution and the Supreme Court
The Poisson Distributioin and the Supreme Court
Journal of the American Statistical Association 31, no. 195 ,(1936), 376-80
W. Allen Wallis
Supreme Court Appointments as a Poisson Distribution
American Journal of Political Science, 26, No.1, February 1982
S. Sidney Ulmer
This is not current news, but since Supreme Court appointments are in the news we felt that these articles might make an interesting class discussion.
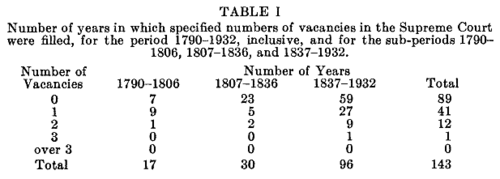
In 1936 Allen Wallis suggested that the number of supreme court appointments in a given year can be approximated by a Poisson distribution. In his Figure 1 Wallis provided the number appointed in each year over the intervals with different numbers of Justices on the Supreme Coourt: 1790-1806 (6) 1807-1836 (7), and 1837-1932 (9). Acually there were 10 in the years 1963 to 1967 which Wallis called "negligible exception."
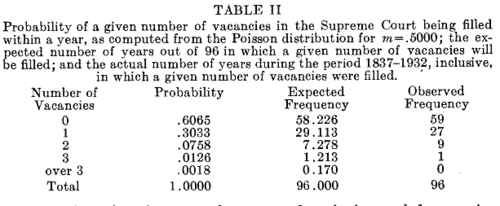
Wallis then restricts himself to the years 1837-1932 and finds that the number of court appoiintments in year can be approximated by a Poisson distrution with mean .5. His results are shown in his Figure 2:
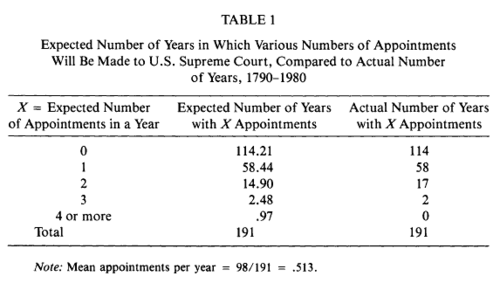
In his article, Sidney Ulmer updated the data to 1980 and also includes data from the early Supreme Courts with 6 and 7 members. Thus his data covers the years 179--1980. His Figure 1 compares actual number of apointments in a year with the expected number of appointments assuming a Poisson distribution with mean 5.13.
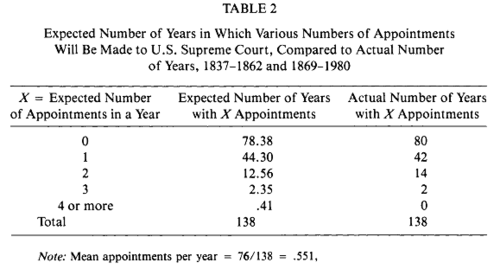
In table 2 Ulmar does the same thing but limited to the 9 year data (1837 to 1980).
testing the goodness of fit, Ullmun argues that the fit with the varying size Supreme Courts is just as good as with fixed size Supreme Courts.
DISCUSSION
(1) Find the probability that a president who serves four years will make 2 or more Supreme Court appointments.
(2) Obtain the data from 1790 to 2005 and make tables corresponding to the Ulman's Tables 1 and 2. Add the tables to this article and also include the data to make it easier to update these results in future years.
Item2
To be added.