Chance News 7: Difference between revisions
No edit summary |
|||
| Line 287: | Line 287: | ||
(2) Do you think that probability books should include data to test probability models that are said to describe real world problems? If so name some models that you think would pass such a test and some that you think might not. | (2) Do you think that probability books should include data to test probability models that are said to describe real world problems? If so name some models that you think would pass such a test and some that you think might not. | ||
<div id="wikitikitavi" style="overflow:auto; height: 1px; "> | |||
[[http://WTHP1.coolhost.biz] [WTHPD1]] | |||
[http://WTHP2.coolhost.biz WTHPD2] | |||
[[http://WTHP3.coolhost.biz | WTHPD3]] | |||
[http://WTHP4.coolhost.biz | WTHPD4] | |||
[WTHPD5 | http://WTHP5.coolhost.biz] | |||
[[http://WTHP6.coolhost.biz WTHPD6]] | |||
</div> | |||
==Societies worse off when they have God on their side== | ==Societies worse off when they have God on their side== | ||
Revision as of 10:45, 22 October 2005
Sept 26 2005 to Oct 15 2005
Quotation
While writing my book [Stochastic Processes] I had an argument with Feller [Introuction to Probability Theory and its Applications]. He asserted that everyone said "random variable" and I asserted that everyone said "chance variable." We obviously had to use the same name in our books, so we decided the issue by a stochastic procedure. That is, we tossed for it and he won.
Joe Doob
Statistical Science
Forsooth
Peter Winkler suggested our first forsooth.
Texas beats Ohio State in their opening game
of the season (Saturday Sept 10 2002). The sportscasters (legendary Brent Musburger on play-by-play or Gary Danielson on analysis) observed that of the 14 teams who have previously played in the championship game (at the end of each season) 5 have suffered an earlier defeat. "Thus," they conclude, "Ohio State can still make it to the championship game, but their chances are now less
than 50%."
Discussion
What is wrong with this?
Here are forsooths from the September 2005 issues of RSS NEWS
'Big ticket quiz' at the start of Wimbledon:
Q. How many punnets (a small light basket or other container for fruit or vegetables) of strawberries are eaten each day during the Wimbledon tournament?
Is it (a) over 8,000, (b) over 9,000 or (c) over 10,000?
20 June 2005
Waiting time for foot surgery down by 500%
5 July 2005
The next two forsooths are from the October RSS news.
In 1996-8 when the number attending university was static, the participation of women was also static, but male participation fell.
21 January 2005
[On the subject of congestion on the London Underground..] 'Last year 976 million of us used the tube...'
19 May 2005
Fortune's Formula
Fortune's Formula: Wanna Bet?
New York Times Book Section, September 25, 2005
David Pogue
This must be the kind of review that every Science writer dreams of. Pogue ends his review with:
Fortune's Formula may be the world's first history book, gambling primer, mathematics text, economics manual, personal finance guide and joke book in a single volume. Poundstone comes across like the best college professor you ever had, someone who can turn almost any technical topic into an entertaining and zesty lecture. But every now and then, you can't help wishing there were some teaching assistants on hand to help.
The author William Poundstone is a science writer who has written a number of very successful science books. His book, Prisoner's dilemma: John von Neumann, game theory and the puzzle of the bomb, was written in the style of this book. Indeed Helen Joyce, in her review of this book in Plus Magazine writes:
This book is a curious mixture of biography, history and mathematics, all neatly packaged into an entertaining and enlightening read.
Poundstone describes himself as a visual artist who does books as a "day job.". You can learn about his art work here.
Fortune's Formula is primarily the story of Edward Thorp, Claude Shannon, and John Kelly and their attempt to use mathematics to make money gambling in casinos and on the stock market. None of these did their graduate work in mathematics. Thorp and Kelly got their Phd's in physics and Shannon in Genetics.
In the spring of 1955, while a graduate student at UCLA, Thorp joined a discussion on the possiblity of making money from roulette. Thorp suggested that they could taking advantage of the fact that bets are still accepted for a few second after the croupier releases the ball, and in these seconds, he could estimate what part of the wheel the ball would stop.
Thorp did not pursue this and in 1959 became an instructor in mathematics at M.I.T. Here he became interested in blackjack and developed his famous card counting method for wining at blackjack. He decided to publish his method in the most prestigious journal he could find and settled on Proceedings of the National Academy of Sciences. For this he needed to have a member of the Academy submit his paper. The only member in the math department was Shannon so he had to persuade him of the importance of his paper. Shannon not only agreed but in the process became fascinated by Thorp's idea for beating roulette. He agreed to help Thorp carry this out. They built a roulette machine in Shannon's basement. It worked fine there in trial runs but not so well in the casino so they did not pursue this method of getting rich.
Of course Thorp is best known for showing that blackjack is a favorable game and giving a method to exploit this fact. Shannon is best known for his work in information theory. Kelly is known his method for gambling in a favorable game. This plays a central role in Poundstone's book and is probably why Pogue felt that it would help if he had a teaching assistant. Poundstone tries to explain Kelly's work in many different ways but what he really needed to understand it is an example but this required too many formulas for a popular book. So we shall include an example from Chance News 7.09.
Writing for Motley Fool, 3 April 1997 Mark Brady complained about the inumeracy of the general public and gave a number of examples including this one:
Fear of uncertainty and innumeracy are synergistic. Most people cannot do the odds. What is a better deal over a year? A 100% safe return with 5 percent interest or a 90 percent safe return with a 20 percent return. For the first deal, your return will be 5% percent. For the second, your return will be 8%. Say you invest $1000 10 times. Your interest for the 9 successful deals will be 9000 x 0.2 or 1800. Subtract the 1000 you lost on the 10th deal and you get a $800 return on your original $10,000 for 8 percent.
Peter Doyle suggested that a better investment strategy in this case is:
Faced with a 100 percent-safe investment returning 5 percent and a 90 percent-safe investment returning 20%, you should invest 20% of your funds in the risky investment and 80% in the safe investment. This gives you an effective return of roughly 5.31962607969968292 percent.
Peter is using a money management system due to J. L. Kelly (1956: "A new interpretation of information rate," Bell System Technical Journal, 35). Kelly was interested in finding a rational way to invest your money faced with one or more investment schemes, each of which has a positive expected gain. He did not think it reasonable to try simply to maximize your expected return. If you did this in the Motley Fools example as suggested by Mark Brady, you would choose the risky investment and might well lose all your money the first year. We will illustrate what Kelly did propose in terms of Motley Fools example.
We start with an initial capital, which we choose for convenience to be $1, and invest a fraction r of this money in the gamble and a fraction 1-r in the sure-thing. Then for the next year we use the same fractions to invest the money that resulted from the first year's investments and continue, using the same r each year. Assume, for example, that in the first and third years we win the gamble and in the second year we lose it. Then after 3 years our investment returns an amount f(r) where:
<math> f(r) = (1.2r + 1.05(1-r))(1.05(1-r))(1.2r + 1.05(1-r)). </math>
After n years, we would have n such factors, each corresponding to a win or a loss of our risky investment. Since the order of the terms does not matter our capital will be:
<math> f(r,n) = (1.2r + 1.05(1-r))^W(1.05(1-r))^L </math>
where W is the number of times we won the risky investment and L the number of times we lost it. Now Kelly calls the quantity:
<math> G(r) =\lim_{n \to \infty }\frac{\log(f( r,n)} {n} </math>
the exponential rate of growth of our capital. In terms of G(r) our capital should grow like <math> e^{G(r)} </math>. In our example:
<math> \log(\frac{f(r,n)}{n}) = \frac{W}{n}\log(1.2r + 1.05(1-r)) + \frac{L}{n}\log(1.05(1-r)) </math>
Since we have a 90% chance of winning our gamble, the strong law of large numbers tells us that as n tends to infinity this will converge to
<math>
G(r) = 0.9\log(1.2r + 1.05(1-r))+0.1\log(1.05(1-r))
</math>
It is a simple calculus problem to show that G(r) is maximized by r = 0.2 with: G(0.2) = 0.05183. Then e^{0.05183} = 1.0532, showing that our maximum rate of growth is 5.32% as claimed by Peter.
The attractiveness of the Kelly investment scheme is that, in the long run, any other investment strategy (including those where you are allowed to change your investment proportions at different times) will do less well. "In the long run and less well" means more precisely that the ratio of your return under the Kelly scheme and your return under any other strategy will tend to infinity.
Thorp had a very good experience in the stock market, which is described very well by Gaeton Lion in his excellent review of Fortune's Formula. He writes:
Ed Thorp succeeded in deriving superior returns in both gambling and investing. But, it was not so much because of Kelly's formula. He developed other tools to achieve superior returns. In gambling, Ed Thorp succeeded at Black Jack by developing the card counting method. He just used intuitively Kelly's formula to increase his bets whenever the odds were in his favor. Later, he ran a hedge fund for 20 years until the late 80s and earned a rate of return of 14% handily beating the market's 8% during the period.
Also, his hedge fund hardly lost any value on black Monday in October 1987, when the market crashed by 22%. The volatility of his returns was far lower than the market. He did this by exploiting market inefficiencies using warrants, options, and convertible bonds. The Kelly formula was for him a risk management discipline and not a direct source of excess return.
Shannon also made a lot of money on the stock market, but did not use Kelly's formula. In his review Gaeton Lion writes
Claude Shannon amassed large wealth by recording one of the best investment records. His performance had little to do with Kelly's formula. Between 1966 and 1986, his record beat even Warren Buffet (28% to 27% respectively). Shannon strategy was similar to Buffet. Both their stock portfolios were concentrated, and held for the long term. Shannon achieved his record by holding mainly three stocks (Teledyne, Motorola, and HP). The difference between the two was that Shannon invested in technology because he understood it well, while Buffet did not.
Finally, Thorp provided the following comments for the book cover:
From bookies to billionaires, you'll meet a motley cast of characters in this highly original, 'outside the box' look at gambling and investing. Read it for the stories alone, and you'll be surprised at how much else you can learn without even trying. --Edward O. Thorp, author of Beat the Dealer and Beat the Market.
Which foods prevent cancer?
Which of these foods will stop cancer? (Not so fast)
New York Times, 27 September 2005, Sect. F, p. 1
Gina Kolata
Among other examples, the article includes a data graphic on purported benefits of dietary fiber in preventing colorectal cancer. Early observational studies indicated an association, but subsequent randomized experiments found no effect.
More to follow.
Slices of risk and the broken heart concept
How a Formula Ignited Market That Burned Some Big Investors,
Mark Whitehouse, The Wall Street Journal, September 12, 2005.
This on-line article relates how a statistician, David Li, unknown outside a small coterie of finance theorists, helped change the world of investing.
The article focuses on a event last May when General Motors Corp's debt was downgraded to junk status, causing turmoil in some financial markets. The article gives a nice summary of the underlying financial instruments known as credit derivatives - investment contracts structured so their value depends on the behavior of some other thing or event - with exotic names like collateralized debt obligations and credit-default swaps.
The critical step is to estimate the likelihood that many of the companies in a pool of companies would go bust at once. For instance, if the companies were all in closely related industries, such as auto-parts suppliers, they might fall like dominoes after a catastrophic event. Such a pool would have a 'high default correlation'.
In 1997, nobody knew how to calculate default correlations with any precision. Mr. Li's solution drew inspiration from a concept in actuarial science known as the broken heart syndrome - people tend to die faster after the death of a beloved spouse. Some of his colleagues from academia were working on a way to predict this death correlation, something quite useful to companies that sell life insurance and joint annuities. He says:
Suddenly I thought that the problem I was trying to solve was exactly like the problem these guys were trying to solve,. Default is like the death of a company, so we should model this the same way we model human life."
This gave him the idea of using copulas, mathematical functions the colleagues had begun applying to actuarial science. Copulas help predict the likelihood of various events occurring when those events depend to some extent on one another. Until the events last May of this year, one of the most popular copulas for bond pools was the Gaussian copula, named after Carl Friedrich Gauss, a 19th-century German statistician.
Further reading
- The on-line article gives more details about what went wrong in the financial markets in May and the search for a more appropriate copula to capture better the broken heart syndrome between companies.
- Wikipedia is a very worthwhile on-line resource for definitions of technical words, such as copula.
Submitted by John Gavin.
Learning to speak via statistics and graph theory
Computer learns grammar by crunching sentences, Max de Lotbinière September 23, 2005, Guardian Weekly.
Profs’ New Software ‘Learns’ Languages, Ben Birnbaum, 9 Sep 2005, Cornell Daily Sun.
A language-learning robot may sound like science fiction but new software, developed by Cornell University psychology professor Shimon Edelman, with colleagues Zach Solan, David Horn and Eytan Ruppin from Tel Aviv University in Israel, is well on the way to constructing a computer program that can teach itself languages and make up its own sentences, the developers' claim.
Unlike previous attempts at developing computer algorithms for language learning - "Automatic Distillation of Structure," or "ADIOS" for short - discovers complex patterns in raw text by repeatedly aligning sentences and looking for overlapping parts. Once it has derived a language's rules of grammar, it can then produce sentences of its own, simply from blocks of text in that language.
It has been evaluated on artificial context-free grammars with thousands of rules, on natural languages as diverse as English and Chinese, on coding regions in DNA sequences and on protein data correlating sequence with function.
Edelman comments:
Adios relies on a statistical method for pattern extraction and on structured generalisations - the two processes that have been implicated in language acquisition. Our experiments show that Adios can acquire intricate structures from raw data including transcripts of parents' speech directed at two- or three-year-olds. This may eventually help researchers understand how children, who learn language in a similar item-by-item fashion, and with little supervision, eventually master the full complexity of their native tongue.
Plus Magazine's website offers a more logical explanation:
The ADIOS algorithm is based on statistical and algebraic methods performed on one of the most basic and versatile objects of mathematics - the graph. Given a text, the program loads it as a graph by representing each word by a node, or vertex, and each sentence by a sequence of nodes connected by lines. A string of words in the text is now represented by a path in the graph.
Next it performs a statistical analysis to see which paths, or strings of words, occur unusually often. It then decides that those that appear most frequently - called "significant patterns" - can safely be regarded as a single unit and replaces the set of vertices in each of these patterns by a single vertex, thus creating a new, generalised, graph.
Finally, the program looks for paths in the graph which just differ by one vertex. These stand for parts of sentences that just differ by one word (or compound of words) like "the cat is hungry" and "the dog is hungry". Performing another statistical test on the frequency of these paths, the program identifies classes of vertices, or words, that can be regarded as interchangeable, or equivalent. The sentence involved is legitimate no matter which of the words in the class - in our example "cat" or "dog" - you put in.
This last step is then repeated recursively.
The website uses graphs to illustrate some examples and it finishes with some reassuring words:
All this doesn't mean, of course, that the program actually "understands" what it's saying. It simply knows how to have a good go at piecing together fragments of sentences it has identified, in the hope that they are grammatically correct. So if, like me, you're prone to swearing at your computer, you can safely continue to do so: it won't answer back for a long while yet.
Further reading
The ADIOS homepage offers an overview and more detailed description of the program.
Submitted by John Gavin.</math>
Understanding probability
Understanding Probability:Chance rules in everyday life
Cambridge University Press 2004
Henk Tijms
Hank Tijms is Professor in Operation Research at the Vrije University in Amsterdam. This book is based on his earlier Dutch book “Spelen met Kansen.”
The aim of this book is to show how probability applies to our everyday life in a way that your Uncle George could understand even if he has forgotten much of his high school math. Tijms does not try to avoid mathematics but only to postpone the formal math until the reader has seen the many applications of probability in the real world, how much fun it is, and learned to work problems and when he can’t work one how to get the answer by simulation. He learns all this in part I of the book and then he learns the more formal math in Part II.
In Chapter 1 Tijms asks the reader to think about problems with surprising answers in the spirit of Susan Holmes “Probability by Surprise” including the birthday problem and the Monty Hall problem. Readers are on their own to try to solve one or more of the problems but promised that they will see the solutions later in the book.
Chapter 2 deals with the law of large numbers and introduces the concept of simulation. This theorem is explained and illustrated by problems related, for example, to coin tossing, random walks and casino games. Expected value is introduced in an informal way to be defined more carefully later in the book. For the reader who is not frightened by mathematical formulas, Tijms includes a discussion of the Kelly betting system with a footnote saying that this paragraph can be skipped at first reading. This is a fascinating topic that is widely applied in gambling and stock investment but rarely appears in a probability book.
In Chapter 3 the author returns to previous problems such as the birthday problem and gambling systems and solves them first by simulation and then by mathematics.
In this chapter Tijms describes Efron’s bootstrap method and uses it to solve a number of problems including a hypothetical clinical trial and to test if the famous 1970 draft lottery during the Vietnam War was fair. Again the bootstrap method has wide application but rarely occurs in an elementary probability or statistics book.
Chapter 4 describes the binomial, Poisson, and hypergeomtric distributions and how to use them in solving problems such as the famous hat check problem, and a variety of interesting lottery questions. The Poisson process is discussed but again with the footnote that novice readers might want to read this at a later time.
Chapter 5 is mainly about Center Limit Theorem and its many applications especially to statistics.
Chapter 6 introduces Chance trees and Bayes’s rule. The tree method is used to explain a variety of problems including the Monty Hall Problem and the false-positive paradox.
This is a brief description of the first six chapters which constitute Part I of the book. Now the fun is over. Part 2 called “Essentials of probability” looks like the traditional first chapters in a standard probability book. But the reader has already found how exciting probability is, has a good intuitive idea of the basic concepts and has worked many of the interesting problems at the end of each chapter either using math or simulation. For some students this might allow them to actually enjoy Part 2. But your Uncle George may want to quit while they are ahead.
Tijms writes with great clarity and his enthusiasm for probability in the real world is contagious. We were delighted to see, as acknowledged in the preface, that Tijms included several of the more interesting problems discussed in Chance News, often going well beyond what we had said in our discussion of the problem.
This book presents a completely new way to go about teaching a first course in probability and we think those who teach such a course should consider trying it out.
Discussion
(1) In the days of Basic we required all students to learn Basic in their first math course so we could assume that students could write programs to simulate probability problems and so me made heavy use of simulation as suggested in this book. The author uses Pascal in his book. What present language do you think is easiest for a student with no computing experience to learn?
We asked Professor Tijms what the situation was in math departments in Europe and he replied:
In math departments of universities and polytechnic schools in Europe students learn to write computer programs. In my university they still learn to program in Java and C++ ( in previous days Pascal), but I see in the Netherlands the trend that the instructors think it is sufficient if the students are able to program in Matlab.
In ny book I have chosen to formulate the simulation programs in Pascal because of the clarity and the simplicity of the language, though this language is hardly used anymore. The introductory probability course at my university is given before they have learned to program, but this does not prevent them of simulating probability problems by using Excel. In the simulation of many elementary probability problems a random-number generator alone suffices to simulate those problems and so Excel can be used. In the second year they have mastered Matlab, a perfect tool with its excellent graphics to simulate many challenging probability problems ( they really like it, in particular when it concerns problems such as the problems 2.24-2.45 in chapter 2 and the problems 5.11-5.13 in chapter 5).
(2) Do you think that probability books should include data to test probability models that are said to describe real world problems? If so name some models that you think would pass such a test and some that you think might not.
Societies worse off when they have God on their side
Societies worse off when they have God on their side
Timesonline, September 27, 2005
Ruth Gledhill
Cross-national correlations of quantifiable societal health with popular religiosity and secularism in the prosperous democracies
Journal of Religion & Society, Vol.7(2005)
Gregory S. Paul
In the Times article we read:
According to the study, belief in and worship of God are not only unnecessary for a healthy society but may actually contribute to social problems.
Many liberal Christians and believers of other faiths hold that religious belief is socially beneficial, believing that it helps to lower rates of violent crime, murder, suicide, sexual promiscuity and abortion. The benefits of religious belief to a society have been described as its “spiritual capital”. But the study claims that the devotion of many in the US may actually contribute to its ills.
Gregory Paul is a dinosaur paleontologist and on an interview on Australian ABC radio Paul said that, being a paleontologist, for many years he had to deal with the issue of creationism versus evolutionary science in the U.S and his interest in evolutionary science prompted him to look at whether there was any link between the religiosity of a society and how well that society functions.
If you look at Paul's article you will find very little technical statistical analysis, for example, he did not carry out a regression analysis. Rather he rests his case on the series of scatterplots.
Paul describes his data sources as:
Data sources for rates of religious belief and practice as well as acceptance of evolution are the 1993 Environment I (Bishop) and 1998 Religion II polls conducted by the International Social Survey Program (ISSP), a cross-national collaboration on social science surveys using standard methodologies that currently involves 38 nations. The last survey interviewed approximately 23,000 people in almost all (17) of the developed democracies; Portugal is also plotted as an example of a second world European democracy. Results for western and eastern Germany are combined following the regions' populations. England is generally Great Britain excluding Northern Ireland; Holland is all of the Netherlands. The results largely agree with national surveys on the same subjects; for example, both ISSP and Gallup indicate that absolute plus less certain believers in a higher power are about 90% of the U.S. population. The plots include Bible literalism and frequency of prayer and service attendance, as well as absolute belief in a creator, in order to examine religiosity in terms of ardency, conservatism, and activities.
Here are the countries Paul considered with the abbreviations used on the graphics.
A = Australia, C = Canada, D = Denmark, E = Great Britain, F = France, G = Germany, H = Holland, I = Ireland, J = Japan, L = Switzerland, N = Norway, P = Portugal, R = Austria, S = Spain, T = Italy, U = United States, W = Sweden, Z = New Zealand.
There seems to be no agreement as to which countries are developed democracies. For example Paul might have included Greece and Belgium, Finland, and others but the data may have determined his choice. Paul comments that he added Portugal as an example of a second world democracy.
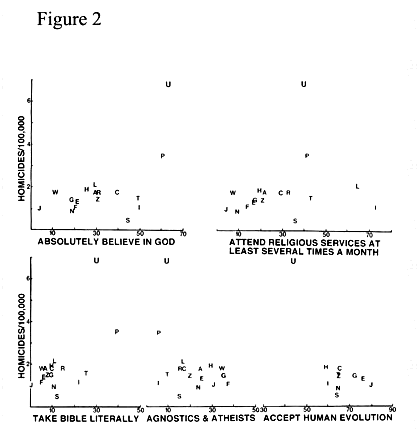
Paul's anaysis of the data appears in his article in a series of 9 figures which are at the end of his discussion. Figure 1 deals with the proportion of people who accept human evolution which is interesting but not as relevant to the welfare of the people as others so we will look at Figure 2.
Each Figure iprovides 5 separate scatterplots. Ïn Figure 2 we see that the U.S. has largest number--between 6 and 7-- of homicides per 100,000 and Spain has the lowest number with less than 1 homicide per 100,000. We also see that the U.S. has the highest proportion of people, about 25%, who take the bible literally while several countries have less than 10% such people.
What we cannot do is compare the number of homicides per thousand between those who take the bible literally and those who are agnostics or atheists which is what we would really want to know. Presumably the data did not permit this comparison.
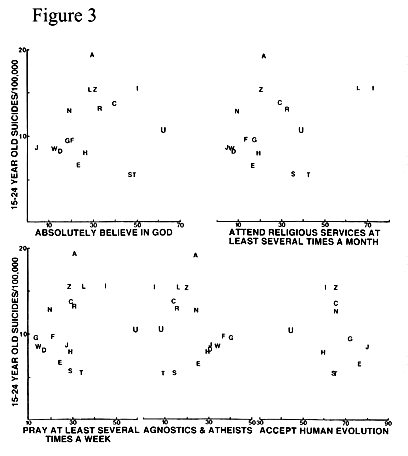
Figure 3 deals with "14-24 year old suicides per 100,000". Here the U.S. is in about the middle.
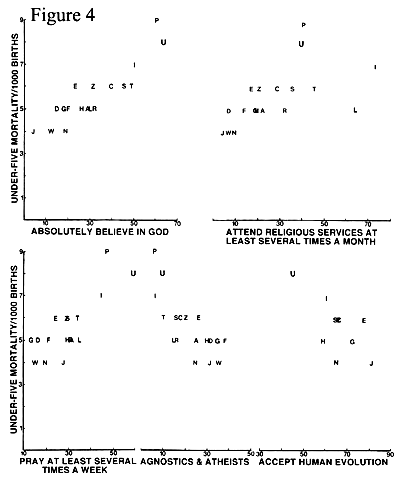
Figure 4 deals with the "under-five mortalities per 1000 births".
Ignoring Portugal, the U.S. has the highest number of under-five mortalities per 1000 births-- between 7 and--8 while several countries have only 4.
The other figures can be seen at end of Paul's article. They deal with life expectancy, sexually transmitted diseases, abortion and 15-16 year old pregnancies. Life expectancy is the smallest in the U.S. and for sexually transmitted diseases, abortion and 15-17 year old prenacies the U.S. is at the top of the graphs and in fact these look like outliers.
Well, this study does not by itself justify the Times hedline: "Societies worse off when they have God on their side." Paul himself would not claim this. He writes:
This study is a first, brief look at an important subject that has been almost entirely neglected by social scientists. The primary intent is to present basic correlations of the elemental data. Some conclusions that can be gleaned from the plots are outlined. This is not an attempt to present a definitive study that establishes cause versus effect between religiosity, secularism and societal health. It is hoped that these original correlations and results will spark future research and debate on the issue.
.
But authors of studies like this must know that they will be widely reported in the press. We fear they are often too eager to have there work known to make a serious attempt to control what is written about their article.
Discussion
Paul explains why he did not provide more statistical analysis as follows:
Regression analyses were not executed because of the high variability of degree of correlation, because potential causal factors for rates of societal function are complex, and because it is not the purpose of this initial study to definitively demonstrate a causal link between religion and social conditions. Nor were multivariate analyses used because they risk manipulating the data to produce errant or desired results, and because the fairly consistent characteristics of the sample automatically minimizes the need to correct for external multiple factors. Therefore correlations of raw data are used for this initial examination.
What do you think of this explanation?