Chance News 27: Difference between revisions
m (→Questions) |
|||
| Line 114: | Line 114: | ||
* [http://www-cpr.maxwell.syr.edu/faculty/smeeding/pdf/JEP%20V5_2006.pdf <em>Poor People in Rich Nations: The United States in Comparative Perspective</em>,] Timothy Smeeding, Syracuse University. | * [http://www-cpr.maxwell.syr.edu/faculty/smeeding/pdf/JEP%20V5_2006.pdf <em>Poor People in Rich Nations: The United States in Comparative Perspective</em>,] Timothy Smeeding, Syracuse University. | ||
* [http://technorati.com/search/http://www.spiegel.de/international/zeitgeist/0,1518,484168,00.html?partnerid=160 Blogs discussing this story,] via Technorati. | * [http://technorati.com/search/http://www.spiegel.de/international/zeitgeist/0,1518,484168,00.html?partnerid=160 Blogs discussing this story,] via Technorati. | ||
* An article by the Wall Street Journal's The Numbers Guy on [http://blogs.wsj.com/numbersguy/does-the-us-lead-in-life-expectancy-223/ life expectancy.] | |||
Submitted by John Gavin. | Submitted by John Gavin. | ||
Revision as of 18:06, 18 November 2007
Quotation
I could prove God statistically. Take the human body alone - the chances that all the functions of an individual would just happen is a statistical monstrosity.
George Gallup
This is from an interesting article about the life of George Gallup: "The Human Yardstick", Williston Rich, Saturday Evening Post January 21,1939, p. 71. The article ends with:
His greatest delusion is that he can forecast the stock market. His greatest fear, that a competitor will enter his field and be dishonest with the figures. His greatest devotion, to his family, his home and his church. He says, "I could prove God statistically--.
Submitted by Laurie Snell
Forsooth
The following Forsooth was in the May 2007 RSS News:
The Times leader of 28 February tells us that taking regular dose of certain vitamins 'can actually increase the risk of mortality by five per cent'. Since the "risk of mortality' is already 100 percent this is very worrying.
AWF Edwards
Cambridge
Da springen drei Rosen, Halb rot und halb weiß
19. Die schöne Müllerin
Franz Schubert,
Submitted and sung by Laurie Snell
Steve Simon provided the following Forsooth:
I'm not sure if this is a "Forsooth" but at the minimum, it is an example of a poorly written survey question. The Kansas City Star newspaper has a poll on its website asking people their opinions about the Harry Potter series of books. The first question asks for an assessment of Severus Snape, one of the main characters in the Harry Potter series. This question is worded "Is Snape good or bad?" and offers the choices "Yes" or "No". As of June 7, there were 33 (29%) votes for "No".
Brian Kelly, the editor of U.S. News, said more than 50 percent of the presidents, provosts and admission deans who were sent the annual survey of colleges’ reputations continued to fill it out. “We think the vast majority of presidents and academics are still supporting the survey,” he said.
20 June 2007
Submitted by Bill Peterson
How to own a random number
God created the integers; all else is the work of man - Leopold Kronecker.
AACS is the copy protection technology used on HD-DVD and Blu-ray discs. The consortium that owns this technology are apparently trying to stop websites and newspapers publishing a specific 128-bit integer that, with suitable software, enables the decryption of video content on most existing HD-DVD and Blu-ray discs. As part of this effort, they have claimed ownership of the encryption key, which means that you cannot use, without written permission, that particular 30-digit integer (in base 10) and several million other unknown keys that they apparently are also claiming ownership of. Not only that, but the numbers in question were chosen randomly so there is no simple way of knowing if your random choice conflicts with theirs, even if their choices were public knowledge.
Further reading
- How to own a random number, BoingBoing blog, 7 May 2007.
- You Can Own an Integer Too — Get Yours Here, Ed Felten, May 7, 2007 — this professor of Computer Science and Public Affairs at Princeton University suggests a way that you can also 'own' your own random integer and hundreds have already done so. He even suggests a use for your number:
Did we mention that a shiny new integer would make a perfect Mother’s Day gift?
- See Amazing mystery of the new AACS key leak, if you want to read the follow-up to this story.
Submitted by John Gavin.
Two probability problems
IBM has a monthly Ponder this challenge which is often a probability problem. The April 2007 Challenge was the following random walk problem.
This month's puzzle concerns a frog who is hopping on the integers from minus infinity to plus infinity. Each hop is chosen at random (with equal probability) to be either +2 or -1. So the frog will make steady but irregular progress in the positive direction. The frog will hit some integers more than once and miss others entirely. What fraction of the integers will the frog miss entirely? You may consider the answer to be the limit as N goes to infinity of the fraction of integers between -N and N a frog starting at -N and randomly hopping as described misses on average. An answer correct to six decimal places is good enough.
You might also want to try the Puzzle for February 2007 which provides another example of the occurrence of the Golden Mean:
Consider the following two person game. Each player receives a random number uniformly distributed between 0 and 1. Each player can choose to discard his number and receive a new random number between 0 and 1. This choice is made without knowing the other players number or whether the other player chose to replace his number. After each player has had an opportunity to replace his number the numbers are compared and the player with the higher number wins. What strategy should a player follow to ensure he will win at least 50% of the time?
Submitted by Laurie Snell
Why have Americans stopped growing?
Bad Health Care, Deficient Welfare Keep Americans Short, Spiegel International, 22 May 2007.
This on-line article, one in a series, claims that US citizens were the tallest in the world up to World War II but since then, US heights have stagnated while Europeans have been getting taller. Furthermore, the average American is now between two and six centimeters shorter than his European counterpart. The article cites a new study, which conjectures that this phenomenon might be explained by differences between health care and the social network systems in various countries. It also suggests a similar result for life expectancy.
The underlying academic paper studies long-term trends in the heights of the US population by combining the results of cross-sectional surveys. The authors analysis is based on the complete set of NHES and NHANES data collected between 1959 and 2004. They used regression analysis to estimate the trend in U.S. heights stratified by gender and ethnicity, holding income and educational attainment constant.
The article asks why the historical correlation between height and wealth is breaking down
The correlation between wealth and height has long been understood, the most recent example coming as Eastern Europeans shot up following the collapse of communism. But why, in the richest country in the world, should growth rates (in height) be stagnating?
This academic study argues that politics may offer an answer. The paper claims that the US average is pulled down by those who struggle to get by, in a country with drastic differences between rich and poor. It claims
Whereas in the US, some 15 percent of the population has no health insurance and those on welfare can barely get by, almost all citizens of northern and western European countries enjoy universal health care and a generous social net. The result is that even those children dependent on welfare in Europe have a sufficient living standard.
The paper mentions that taller people have higher incomes, on average, but is unsure about the direction of causation. Is spite of this, the US population height has been stable since 1950 even though prosperity continued to rise, something that will require further work to explain, according to the authors:
Quite a bit more needs to be done to determine the relationship between social standards and height. In short, the richest are neither the tallest nor the healthiest. Why that is so must be explained.
Questions
- Today, Americans are between two and six centimeters shorter than the Dutch but in the mid-19th centaury the reverse was the case. How reliable do you think data from 150 years ago is, in this case? What questions might you ask to ensure that any comparisons between cross sectional studies, over such a long period of time, are fair? How large do you think the samples sizes might have to be to justify such claims?
- The authors claim an association between height and health but also mention an association between health and life expectancy. Height is easy to measure and fixed (between ages 20-50) but life expectancy appears not to be. Is it plausible to speculate about what average height might tell us about average life expectancy? Might it be easier for health educators and policy makers to focus on height as a simpler and more transparent measure of health than life expectancy?
- Similar to the previous question, there is a negative correlation between population height and population illiteracy and population height and income inequality. Would height serve as a good proxy for the overall well-being of a population? If so, why aren't trends in population height used by policy makers more often?
- Other factors that might influence the relation between height and health, such as nutritional intake, incidence of disease and availability of medical services, were not felt to be material in developed countries. Why might this be? Might these factors have been more relevant in the past? How difficult do you think it would be to reliably extract such measures from historical data?
- The paper briefly mentions a negative association between population height and population density, allowing for social status. Speculate on how you might investigate such a relationship.
- If height seems like an attractive proxy for health, how might you handle the fact that a population's average height grows with age between 0 and about 20 and shrinks with age above about age 50? Without such adjustments, is it necessary to wait 20 years for each generation's final height to stabilize before drawing conclusions about their future health and life expectancy?
- For future studies, speculate on how genetic information might gradually replace height as a proxy for future health. What are genetics’ relative merits compared to height?
Further reading
- Underperformance in Affluence: The Remarkable Relative Decline in U.S. Heights in the Second Half of the 20th Century, Komlos, Benjamin E. Lauderdale (2007), Social Science Quarterly 88 (2), 283–305 (another link to the pdf). This new study published in the current issue of the Social Science Quarterly by researchers from Princeton University in the US and the University of Munich in Germany indicates that the difference may have to do more with politics than biology.
- America's Middle Class Has Become Globalization's Loser, Gabor Steingart, Speigel International, 24 Oct 2006 - excerpted from the German best-seller World War for Wealth: The Global Grab for Power and Prosperity by Speigel editor Gabor Steingart.
- Poor People in Rich Nations: The United States in Comparative Perspective, Timothy Smeeding, Syracuse University.
- Blogs discussing this story, via Technorati.
- An article by the Wall Street Journal's The Numbers Guy on life expectancy.
Submitted by John Gavin.
A short film exploring relative sizes
On the topics of visualization and scaling, this short film visualizes the size of 'things' and the effect of then adding a zero to the scale. With every passing 10 seconds, the view is 10 times wider: starting with one meter - a person lying on the ground - to 10^24 - the universe. It then reverses the view down to a subatomic particle, 10^-14. A journey of 40 powers of ten.
Further reading
- The video was made by Charles and Ray Eames at IBM.
- If you have trouble with the link above, try searching for Powers of Ten.
- I found the original link at specialten.tv - wait for the page to load, then click on the link labeled Top Ten, in the top left of the page, to get a drop down list, then click on Powers of ten, which is fifth on the list.
Submitted by John Gavin.
So you think you know how to give a statistics lecture
The scoop on data visualization, Statistical Computing and Graphics Newsletter, June 2007.
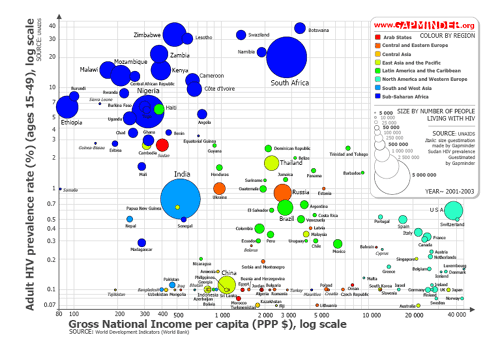
Another video article. This video shows a 20 minute lecture by Hans Rosling, a medical doctor and a professor of International Health at the Karolinska Institute in Stockholm, on the topic of debunking third-world myths.
It shows interactive data-analysis and presentation techniques, to communicate complex data in a clear and intuitive manner, via moving bubbles and flowing curves, along with a few jokes. The image on the right shows a snapshot that is typical of the dynamic images discussed in the video.
To quote from the TED website:
You've never seen data presented like this. With the drama and urgency of a sportscaster, Hans Rosling debunks myths about the so-called "developing world" using extraordinary animation software developed by his Gapminder Foundation. The Trendalyzer software (recently acquired by Google) turns complex global trends into lively animations, making decades of data pop. Asian countries, as colorful bubbles, float across the grid - toward better national health and wealth. Animated bell curves representing national income distribution squish and flatten. In Rosling's hands, global trends - life expectancy, child mortality, poverty rates - become clear, intuitive and even playful.
Rosling argues that The West's view of the third world is based on ill-informed and preconceived notions that differ radically from the reality and that such misconceptions result in weak policy decisions. The speaker asserts that we have generally underestimated the social change in Asia, over the last forty years, and that such social change is a prerequisite for economic change. He also claims that the concept of a developing country is flawed because the variation within the standard country groups, like 'Africa', is so high.
Business Week Online commented
Rosling believes that making information more accessible has the potential to change the quality of the information itself.
Questions
- The speaker is not a statistician. Would you have recognized this before watching the video? His graphics do not emphasize the underlying analysis, does this matter? Do you think the validity of the figures from so many different countries over so many years is credible? Would it affect the overall conclusions from his talk? Do you know where to go to track down some comparable figures? Would you have guessed that there is over a terabyte of public data on national and international statistics, from sources such as the UN, national statistics offices, NGOs, Amnesty and others?
- The speaker claims you can move much faster if you're healthy first than if you're wealthy first. Does the material in his presentation support this assertion? What further details would you like to see?
- Can you find other similar statistical talks on the TED website, inspired talks by the world's greatest thinkers and doers or elsewhere? What is your current top choice?
Further reading
- Source - The scoop on data visualization, Statistical Computing and Graphics Newsletter, page 11, June 2007.
- This source also highlighted what the national statistical offices of several countries are doing to improve statistical literacy and interest in their national statistics data by their citizens, using many different kinds of animation software.
- This link allows you to interactively play with the data in the video.
- Note that Flash is typically required so you may need to install the latest version etc.
- This handouts page offers several pdfs with colorful graphs that can be printed out as posters.
- For example, you can click on this AIDS chart to get the underlying image.
- There is a 200mb high quality version of the video, if you have the bandwidth.
- Here is another presentation from Gapminder.
- Rosling recently edited Global Health: An Introductory Textbook, 2006.
- Rosling has a few claims to fame, in addition to his software,
- He ended this talk by swallowing a sword, literally.
- He is one of the few sword-swallowers active in Sweden.
- He discovered the paralytic disease Konzo, which earned him a PhD.
- In 2005, he co-founded the non-profit Gapminder Foundation, which developed the Trendalyzer software whose aim is to promote a fact based world view through the increased use, understanding and visualization of freely accessible public international statistics. The interactive Flash animations are freely available from the Foundation's website.
- Google has acquired Hans Rosling's Trendalyzer software, with the intention to scale it up and make it freely available for public statistics.
- He ended this talk by swallowing a sword, literally.
- Hans Rosling's blog and his wikipedia entry.
Submitted by John Gavin.
Statistics dampen feelings of compassion
Genocide: When compassion fails, Paul Slovic, New Scientist, 07 April 2007.
If I look at the mass, I will never act. If I look at the one, I will. Mother Teresa
This New Scientist article asserts that people do not value lives consistently, when donating to charitable causes. In particular, the authors claim that statistics can dissipate any emotion we might feel towards a victim, by comparing a 'statistical' victim to an identifiable victim.
Examples of statistical victims are:
- Food shortages in Malawi are affecting more than 3 million children.
- In Zambia, severe rainfall deficits have resulted in a 42 percent drop in maize production from 2000. As a result, an estimated 3 million Zambians face hunger.
- Four million Angolans -- one third of the population -- have been forced to flee their homes.
- More than 11 million people in Ethiopia need immediate food assistance.
In contrast, an example of an identifiable victim is:
- Any money that you donate will go to Rokia, a 7-year-old girl from Mali, Africa. Rokia is desperately poor, and faces a threat of severe hunger or even starvation. Her life will be changed for the better as a result of your financial gift.
Studies have shown how people are more willing to aid specific individuals than those who are unidentified or simply listed as statistics, the 'identifiable victim' effect.
In a series of field experiments, the authors claim that teaching people to recognize the discrepancy in giving toward identifiable and statistical victims had perverse effects: individuals gave less to identifiable victims but did not increase giving to statistical victims, resulting in an overall reduction in caring and giving. Thus, it appears that, when thinking analytically, people discount sympathy towards identifiable victims but fail to generate sympathy toward statistical victims.
In a related paper by Small and Loewenstein, people felt less compassion and donated less aid towards a pair of victims than to either individual alone.
Questions
- Do you agree with the article's assertion that people are more generous toward specific identified victims than toward unidentifiable 'statistical' victims? If so, why do you think this might be? For example, as individuals, do we feel powerless to fight systemic evils but able to help individual people?
- What techniques might be used when presenting statistics so that an emotional response, sufficient to motivate action, can be created and maintained?
- Joseph Stalin was quoted as saying A single death is a tragedy; a million deaths is a statistic. Is Stalin commenting on the same issue as the New Scientist article?
Further reading
- Learning about the identifiable victim effect, Deborah A. Small, University of Pennsylvania, George Loewenstein, Carnegie Mellon University and Paul Slovic, Decision Research.
- The devil you know: the effects of identifiability on punishment, Deborah A. Small of the University of Pennsylvania and George Loewenstein of Carnegie Mellon University.
Submitted by John Gavin.
Correlation and tonal languages
Words in code, The Economist, 31st May 2007.
Speaking in tones? Blame it on your genes, Mark Henderson, Science Editor , The Times Online (UK)
A Genetic Basis for Language Tones?, Nikhil Swaminathan, Scientific American, 29 May 2007.
Is Your Tongue in Your Genes?, Michael Balter, ScienceNOW Daily News, 29 May 2007.
Genes May Influence Language Learning, Study Suggests, Mason Inman, National Geographic News, 29 May 2007.
A widely-reported academic paper discusses a statistical study of the relationship between the geographical distribution of two human genes and the geographical distribution of tonal languages. From this, the authors, Dan Dediu and D. Robert Ladd, at the University of Edinburgh, assert a genetic basis for people's ability to learn a tonal language. Ladd said
I looked at maps of the distributions of the old and new versions of the genes. And I said, that looks like the distribution of tonal languages.
In effect, the language people speak is at least partly determined by genes, rather than just experience alone.
About half the world's languages are tonal languages, in which the pitch or tone of words and syllables makes a difference to word meaning. Examples include: Chinese, Thai, Yoruba, and Zulu. In Mandarin Chinese, for example, the syllable "ma" can take on several unique meanings: when it's pronounced with a single high-pitched tone, "ma" means "mother." But when it has a low-pitched lilt in the middle, it means "horse", making it a word you don't want to mispronounce. In contrast, English is a non-tonal language.
This split is unevenly distributed: tonal languages are the norm in sub-Saharan Africa and are common in Southeast Asia and among Native American languages especially in parts of Central and South America. Non-tonal languages are the norm in Europe and Central, South and West Asia, and among the aboriginal languages of Australia. If your ancestors were all European, with mostly nontonal languages in Europe, you have a better than even chance of carrying the two new genes.
The two genes in question have emerged in the human population only very recently, 6,000 to 37,000 years ago. This implies that the very first human languages were probably tonal, sounding more like Zulu or Chinese than French or English. Furthermore, these new genes seem to be spreading quickly in the human species, suggesting that they are favoured by natural selection.
The author’s hypothesis concerns the relationship between a typological linguistic feature (namely, tone) and the "derived" alleles (variants) of two human genes. They tested the hypothesis by gathering genetic data, in the form of allele frequencies, and linguistic data, in the form of values of typological features from 49 populations around the world.
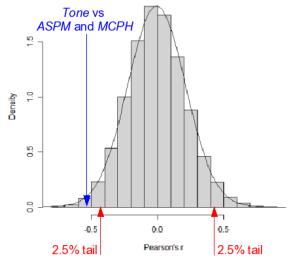
Next they calculated the correlation between tone and each of the alleles separately. But it may be that genes generally correlate with the typological features of language because of patterns of past migration and contact between peoples speaking different languages. Therefore Dediu and Ladd wanted to make sure that the correlation is 'significant' not only in the standard statistical sense, but also that it is unusual when compared to other correlations between genes and typological features. So for the same 49 populations, they gathered frequency data for 983 alleles and values for 26 typological features, such as the number of consonants or the use of inflections, in order to see in which manner genes and typological features tend to behave. They show that the correlations between all pairs of genes and typological features follows a normal distribution around zero. See the graph on the right.
This means that, as expected, there is no general correlation between genes and linguistic features, so language features are unlikely to be affected by genes. But the relation between tone and the two genes under study was confirmed to be especially strong in all the analyses.
It’s because there generally isn’t a correlation between population genetics and language typology that the correlation we’ve found may be interesting
one of the authors claims.
Pearson's correlation was calculated when considering each of the two genes separately. In addition, the authors used logistic regression to consider the impact of both genes together, to estimate how the frequency of the two genes in a population predicts its language tonality.
Ladd said
What we have found suggests that these genes might have a very small effect on individuals, and a larger effect on the populations in which they live. As the language is passed on culturally, it would then be more likely to develop along one path than the other.
Remarkable correlations could happen by chance. Because they compute a large number of statistical measures, the significances (p-values) of the results had to be adjusted. (When computing, for example, 1000 correlations, just by chance 10 will turn out to be significant for an alpha level of 0.01.) So the paper adjusts all its p-values .
Ladd was cautious with his conclusions:
The research had so far found only an association that appears to be more than chance, and that more work was needed to confirm a causal effect.
Questions
- Languages from the Americas were excluded. Why do you think the authors did this?
- Speculate how you think the authors take into account the fact that neighboring populations tend to share both the same genes and languages?
- The authors transform their data into distances to control for geography and history. They based geographic distance between populations on land distances rather than 'as the crow flies', why do you think this measure might be more appropriate?
- Person's correlation measures the strength of a linear relationship between two variables. Why do you think linearity is justified in this case? The Manel test is used to assess its significance, are you familiar with this type of permutation test?
- Other factors might cause an unusual correlation to occur include prehistoric migration. Can you think of any other factors that might result in the observed unusual correlations?
- Can you think of any other tests the authors might have considered? Why did the authors need to consider the combined impact of the two genes? What benefits does a logistic regression offer over correlation statistics? Is the extra complexity justified in this case?
Further reading
- The underlying academic paper by Dan Dediu and D. Robert Ladd, University of Edinburgh, is available from Proc. Natl. Acad. Sci. USA (subscription required).
- Due to the amount of press coverage of this paper, the authors have written up a less technical description of their paper. The bottom of this summary page lists other media articles.
- They also offer a separate non-technical summary of their statistical procedures.
Submitted by John Gavin
Seven holes in one in 14 weeks. What are the odds?
113,527,276,681,000,000 to 1
Those were the odds local golfer Jacqueline Gagne could make seven holes in one in 14 weeks.
The Desert Sun (Palm Springs) April 28
Larry Gohannan
April 28, 2007
Lee Sechrest suggested this article which is a good example to discuss how we should react to a claim that an event with an unbelievably small probability has occurred.
Jacqueline Gagne is a 47 year old computer programmer who retired and moved to Rancho Mirage, California. Here she continued her love of sports by playing golf four or five times a week. Between January and May she made seven holes in one. From the Desert Sun article we read:
Before she recorded her eighth this week, Professor Mike McJilton of the College of the Desert Math and Science Department calculated the odds of making seven aces in approximately 65 rounds (five rounds a week for 13 weeks) as Gagne did is just under 114 million billion to 1. As a decimal number, the chance of making the seven aces is 0.0000000000000000088
McJilton used the Poisson Distribution, presumably as an approximation to the binomial distribution. For this he needed to know the probability that a reasonable golfer makes a hole in one in a round. There have been many attempts to estimate this. You can read about this here. It is said here that the Golf Digest hired Francis Sheid, the retired chairman of the math department at Boston University, to calculate the odds using the latest and best information available. The odds Scheid came up with were 5,000 to 1 for a "low-handicapper," and 12,000 to 1 for an "average player". These were higher than previous estimates. Using Mathematca and the Binomial Distribution with p = 1/5000 and n = 65 we find that the probabiliy of 7 success agrees with McJilton’s result.
The next calculation of such odds was discussed in the Sports News May 24, 2007. By this time Gagne has made 10 holes in one in 16 weeks. Here we read:
We asked one of the world's foremost mathematicians, Joseph B. Keller, professor emeritus of mathematics and mechanical engineering at Stanford, to compute the odds of making 10 aces in 80 rounds (using a previous finding by "Golf Digest" that the odds of an average player making an ace in any given round are 1 in 5,000). Keller's answer: "Roughly two chances out of 10 followed by 24 zeros. This is the same chance as picking one particular molecule out of all the molecules in 50 gallons of air."
By June 3 Jacqueline had made 14 holes in one in the past 5 months. Again using the Binomial model and Mathematica we find the probability of this event is .0000000000000000000000000000000000003.
Of course people were suspicious of a fraud but they were able to find witnesses to all of her holes in one. Her authenticity gained further support when an ABC TV station sent a crew to interview her and she hit a hole in one while they were there. You can see this hole in one here.
There has been a lot of discussion about this event. See in particular the discussion by Carl Bialick and the comments of his readers at the "Numbers Guy" Blog. Carl Bialik writes a column called The Numbers Guy for the Wall Street Journal and maintains the "Numbers Guy" Blog.
We like the following remarks made by Professor Sechrest when he suggested this topic:
The accounts of the statistical estimation procedures were quite interesting and represented something of a tour-de-force in calculating probabilities. What seemed to me to be odd, however, is that no one recognized, at least not explicitly, that the probability of such a record, once beyond a certain point, ceases to be interesting. One simply reaches a point at which it is evident that the woman has some special skill. Packing on further improbabilities does not provide any new information. It is my understanding that she came to the attention of people for her golfing prowess some time ago, i.e., before she reached ten, further supporting the conclusion that she has more than luck going for her.
I have a pair of loaded dice that I use for demonstrations from time to time. After I have rolled about six sevens out of, say, nine tries, everyone agrees that the dice are loaded. Going ahead to roll another six sevens does not impress anyone as remarkable.
Discussion:
(1) Of course we only hear about unusual events so we should really have a bigger sample space. How could this be done for this event?
(2) Keith Devlin is reported to have said "The only justifiable probability is 100% since the event happened. What do you think about this?
(3) The estimate of 1/5000 for getting a hole in one for low handicapped players was probably based on the assumption that the distribution for the number hole in ones for golfers in this class is a normal distribution. Greg Leibon suggested that there might be a very few players who have a good chance of hitting a hole in one so that a power law might be more appropriate. Would this make Jacqueline Gagne's achievement more plausible?
(3) What odds would you give for Jacqueline getting a hole in one in her next round of play?
Submitted by Laurie Snell