Chance News 22: Difference between revisions
| (8 intermediate revisions by 3 users not shown) | |||
| Line 49: | Line 49: | ||
An Unwelcome Discovery, by Jeneen Interlandi, The New York Times, October 22, 2006. | An Unwelcome Discovery, by Jeneen Interlandi, The New York Times, October 22, 2006. | ||
The New York Times has an informative summary of a recent scandal involving a prominent researcher at the University of Vermont, Eric Poehlman. The Poehlman scandal represents perhaps the biggest | The New York Times has an informative summary of a recent scandal involving a prominent researcher at the University of Vermont, Eric Poehlman. The Poehlman scandal represents perhaps the biggest case of research fraud in recent history. | ||
<blockquote>He presented fraudulent data in lectures and in published papers, and he used this data to obtain millions of dollars in federal grants from the National Institutes of Health — a crime subject to as many as five years in federal prison.</blockquote> | <blockquote>He presented fraudulent data in lectures and in published papers, and he used this data to obtain millions of dollars in federal grants from the National Institutes of Health — a crime subject to as many as five years in federal prison.</blockquote> | ||
| Line 98: | Line 98: | ||
<blockquote>“There are conflicting influences on a university where they are the co-grantor and responsible to other investigators,” says Stephen Kelly, the Justice Department attorney who prosecuted Poehlman. “For the system to work, the university has to be very ethical.”</blockquote> | <blockquote>“There are conflicting influences on a university where they are the co-grantor and responsible to other investigators,” says Stephen Kelly, the Justice Department attorney who prosecuted Poehlman. “For the system to work, the university has to be very ethical.”</blockquote> | ||
Poehlman himself was careful and chose areas where fraud would be especially difficult to detect. He specialized in presenting longitudinal data, data that is very expensive to | Poehlman himself was careful and chose areas where fraud would be especially difficult to detect. He specialized in presenting longitudinal data, data that is very expensive to replicate. He also presented research results that confirmed what most researchers had suspected, rather than results that would undermine existing theories of nutrition. | ||
At his sentencing, Poehlman was sentenced to one year and one day in federal prison, making him the first researcher to serve time in jail for research fraud. | At his sentencing, Poehlman was sentenced to one year and one day in federal prison, making him the first researcher to serve time in jail for research fraud. | ||
| Line 123: | Line 123: | ||
Kay's article follows up on the reaction to that report. | Kay's article follows up on the reaction to that report. | ||
He tells us that accurate public information is a prerequisite of democracy, | He tells us that accurate public information is a prerequisite of democracy, government statisticians are honest people but ministers (politicians) needs are often for propaganda rather than facts. | ||
Kay claims that decentralisation of responsibility for the production of official statistics has created a two-tier system in the UK. | Kay claims that decentralisation of responsibility for the production of official statistics has created a two-tier system in the UK. | ||
<blockquote> | <blockquote> | ||
statistics produced by the Office for National Statistics (ONS), which operates to internationally agreed criteria, are of higher quality than those produced by (government) departments. | statistics produced by the Office for National Statistics (ONS), which operates to internationally agreed criteria, are of higher quality than those produced by (government) departments. | ||
</blockquote> | </blockquote> | ||
The proposal to hand | The proposal to hand responsibility for all official statistics to the ONS was rejected, | ||
as were the suggestions for greater independence, made by bodies such as the Statistics Commission and the Royal Statistical Society, | as were the suggestions for greater independence, made by bodies such as the Statistics Commission and the Royal Statistical Society, | ||
* separating statistical information from political statements, | * separating statistical information from political statements, | ||
| Line 134: | Line 134: | ||
* giving parliament a defined role in the appointment of the National Statistician. | * giving parliament a defined role in the appointment of the National Statistician. | ||
Instead, the | Instead, the latest news is that the ONS will be demoted to a non-ministerial department. | ||
The worst news is the abolition of the Statistics Commission, which reviews all government statistics, and has made itself unpopular with government by proving itself robustly independent. | The worst news is the abolition of the Statistics Commission, which reviews all government statistics, and has made itself unpopular with government by proving itself robustly independent. | ||
| Line 143: | Line 143: | ||
==An example of Simpson's Paradox== | ==An example of Simpson's Paradox== | ||
Study finds wealth inequality is widening worldwide<br> | [http://www.nytimes.com/2006/12/06/business/worldbusiness/06wealth.html Study finds wealth inequality is widening worldwide]<br> | ||
''New York Times'', Dec. 6, 2006, C-3<br> | ''New York Times'', Dec. 6, 2006, C-3<br> | ||
Eduardo Porter | by Eduardo Porter | ||
The article contains stats from a 2000 report on wealth distribution by | The article contains stats from a 2000 report on wealth distribution by | ||
| Line 159: | Line 159: | ||
==Predecessors of Poehlman== | ==Predecessors of Poehlman== | ||
Steve Simon's | Steve Simon's post, "I wasn't making up data, I was imputing!" is quite interesting and informative. Nevertheless, some elaboration is in order regarding fraud and Simon's statement that "The Poehlman scandal represents perhaps the biggest case of research fraud in recent history." | ||
The term "recent history" is sufficiently elastic to permit quoting myself in the 1980s: <blockquote>Admittedly Slutsky is an extreme example...even after the investigation [proving fraud in many of his papers]...Robert G. Slutsky was [still] given credit for [an additional] 77 publications in his seven years with [the University of California, San Diego]...in 1984 he published at the astonishing rate of one paper every ten days..Slutsky's phenomenal productivity was encouraged, applauded and rewarded...John R. Darsee [another cardiologist but at Harvard], had about 100 papers in a period of two years and his undoing in 1981 was colleagues who secretly saw him forging the data.</blockquote> | The term "recent history" is sufficiently elastic to permit quoting myself in the 1980s: <blockquote>Admittedly Slutsky is an extreme example...even after the investigation [proving fraud in many of his papers]...Robert G. Slutsky was [still] given credit for [an additional] 77 publications in his seven years with [the University of California, San Diego]...in 1984 he published at the astonishing rate of one paper every ten days..Slutsky's phenomenal productivity was encouraged, applauded and rewarded...John R. Darsee [another cardiologist but at Harvard], had about 100 papers in a period of two years and his undoing in 1981 was colleagues who secretly saw him forging the data.</blockquote> | ||
| Line 198: | Line 198: | ||
* To be among the richest 10% of adults in the world required $61,000 in assets. | * To be among the richest 10% of adults in the world required $61,000 in assets. | ||
* More than $500,000 was needed to belong to the richest 1% (37 million members). | * More than $500,000 was needed to belong to the richest 1% (37 million members). | ||
* Household wealth amounted to $125 trillion in the year 2000, equivalent to roughly three times the value of total global production (GDP) or to $20,500 per person. Adjusting for differences in the cost-of-living across nations raises the value of wealth to $26,000 per capita when measured in terms of purchasing power parity dollars | * Household wealth amounted to $125 trillion in the year 2000, equivalent to roughly three times the value of total global production (GDP) or to $20,500 per person. Adjusting for differences in the cost-of-living across nations raises the value of wealth to $26,000 per capita when measured in terms of purchasing power parity dollars. | ||
* Wealth levels vary widely across countries: ranging from $37,000 per person for New Zealand and $70,000 for Denmark to $127,000 for the UK (for high-income OECD nations). | * Wealth levels vary widely across countries: ranging from $37,000 per person for New Zealand and $70,000 for Denmark to $127,000 for the UK (for high-income OECD nations). | ||
* North America has only 6% of the world adult population, yet it accounts for 34% of household wealth. | * North America has only 6% of the world adult population, yet it accounts for 34% of household wealth. | ||
| Line 212: | Line 212: | ||
The authors define wealth to mean 'the value of physical and financial assets less debts', | The authors define wealth to mean 'the value of physical and financial assets less debts', | ||
so wealth represents the ownership of capital. | so wealth represents the ownership of capital. | ||
They claim that capital is widely believed to have a disproportionate impact on household | They claim that capital is widely believed to have a disproportionate impact on household well-being and economic success, and more broadly on economic development and growth. | ||
The authors use the [http://en.wikipedia.org/wiki/Gini_coefficient Gini value] to measure inequality on a scale from zero to one. They claim that wealth is shared much less equitably than income. Income inequality ranges from 35% to 45% and wealth inequality are usually between 65% and 75% (e.g. zero would mean everyone has the same income and one means that one person has all the income and everyone else has none). | The authors use the [http://en.wikipedia.org/wiki/Gini_coefficient Gini value] to measure inequality on a scale from zero to one. They claim that wealth is shared much less equitably than income. Income inequality ranges from 35% to 45% and wealth inequality are usually between 65% and 75% (e.g. zero would mean everyone has the same income and one means that one person has all the income and everyone else has none). | ||
| Line 227: | Line 227: | ||
===Questions=== | ===Questions=== | ||
* A presentation format | * A presentation format consisting of a list of such point-estimate statistics seems disjointed, as it swaps repeatedly between statistics for the richest and the poorest. Could the data be more meaningfully presented via a distribution? | ||
* The graph shows a discrete five point distribution. Is such a split of the data into buckets such as 'under 2000' and 'over 50000' meaningful? | * The graph shows a discrete five point distribution. Is such a split of the data into buckets such as 'under 2000' and 'over 50000' meaningful? | ||
* Mapping the output to countries via colours, shows the geographic distribution of the underlying variable, wealth. What is misleading about this graph? How might countries be scaled in size to better relflect the data. | * Mapping the output to countries via colours, shows the geographic distribution of the underlying variable, wealth. What is misleading about this graph? How might countries be scaled in size to better relflect the data. | ||
| Line 240: | Line 240: | ||
Cornelia Dean | Cornelia Dean | ||
This article appeared as the US Supreme Court began hearing its first case involving global warming. A case has been filed against the federal government by a group of state and local | This article appeared as the US Supreme Court began hearing its first case involving global warming. A case has been filed against the federal government by a group of state and local governments, together with environmental groups. These plaintiffs charge that that the Environmental Protection Agency, by refusing to regulate greenhouse gas emissions, is failing to enforce the Clean Air Act. | ||
Some of the arguments involve legal technicalities, such as whether the states actually have standing to bring such a suit. But the present article is concerned with the scientific evidence, and what responsibility the Court has to educate itself about the scientific underpinnings of a case. The article draws the following distinction | Some of the arguments involve legal technicalities, such as whether the states actually have standing to bring such a suit. But the present article is concerned with the scientific evidence, and what responsibility the Court has to educate itself about the scientific underpinnings of a case. The article draws the following distinction between statistical and legal standards for proof: | ||
<blockquote> | <blockquote> | ||
| Line 248: | Line 248: | ||
</blockquote> | </blockquote> | ||
The article provides some historical references on how the Court has previously viewed scientific testimony, beginning discussion of the 1923 Frey case on lie detectors, which introduced the "general acceptance" standard. This was updated in the 1993 case Daubert v. Merrell Dow Pharmaceuticals, which involved the drug Bendectin and | The article provides some historical references on how the Court has previously viewed scientific testimony, beginning with discussion of the 1923 Frey case on lie detectors, which introduced the "general acceptance" standard. This was updated in the 1993 case Daubert v. Merrell Dow Pharmaceuticals, which involved the drug Bendectin and its possible association with birth defects. The Court introduced the concepts of "testability" and "peer review" into its deliberations on science. In the 1998 case General Electric Company v. Joiner, the Court ruled that "judges could reject evidence if there was simply too great a gap between 'the data and the opinion proffered.'" | ||
The main thrust of the article, however, is that the Court still has been too slow to keep up with the explosion of scientific knowledge, which can be expected to play an ever larger role in future cases. For example, when corrected on a technical point in the discussion about carbon dioxide, Justice Scalia responded, "Troposphere, whatever. I told you before I'm not a scientist." | The main thrust of the article, however, is that the Court still has been too slow to keep up with the explosion of scientific knowledge, which can be expected to play an ever larger role in future cases. For example, when corrected on a technical point in the discussion about carbon dioxide, Justice Scalia responded, "Troposphere, whatever. I told you before I'm not a scientist." | ||
Latest revision as of 22:00, 21 January 2012
Quotations
It would be hard to make a probability course boring.
William Feller
Personal comment to Laurie Snell
Apart from Fred, [an obstreperous rat in her psychology lab] I was sick of trying to master statistics. I had a mental block when it came to any form of mathematics. 'Rats and stats,' I complained to a fellow student one day, 'I came here to learn about people.' I wasn't the only student disgruntled. Many complained but to no avail.
Sally Morgan in her book, My Place
The risk of going into cardiac arrest as a spectator, he [Dr. Siegal of Massachusetts General Hospital] said, is only about one in a million. (The applicable studies of spectators involved Super Bowl fans.)
Forsooth
NOAA's heating degree day forecast for December, January and February projects a 2 percent warmer winter than the 30 year average
The following Forsooths are from the November 2006 RRS NEWS.
At St John's Wood station alone, the number of CCTV cameras has jumped from 20 to 57, an increase of 300 per cent.
Metro
3 May 2006
Now 78% of female veterinary medicine students are women, almost a complete turn-around from the previous situation.
The Herald (Glasgow)
4 May 2006
Drought to ravage half the world within 100 years
Half the world's surface will be gripped by drought by the end of the century, the Met Office said yesterday.
Times online
6 October 2006
I wasn't making up data, I was imputing!
An Unwelcome Discovery, by Jeneen Interlandi, The New York Times, October 22, 2006.
The New York Times has an informative summary of a recent scandal involving a prominent researcher at the University of Vermont, Eric Poehlman. The Poehlman scandal represents perhaps the biggest case of research fraud in recent history.
He presented fraudulent data in lectures and in published papers, and he used this data to obtain millions of dollars in federal grants from the National Institutes of Health — a crime subject to as many as five years in federal prison.
The first person to speak up about the possibility of fraud in Poehlman's work was one of his research assistants, Walter DeNino.
The fall that DeNino returned to the lab, Poehlman was looking into how fat levels in the blood change with age. DeNino’s task was to compare the levels of lipids, or fats, in two sets of blood samples taken several years apart from a large group of patients. As the patients aged, Poehlman expected, the data would show an increase in low-density lipoprotein (LDL), which deposits cholesterol in arteries, and a decrease in high-density lipoprotein (HDL), which carries it to the liver, where it can be broken down. Poehlman’s hypothesis was not controversial; the idea that lipid levels worsen with age was supported by decades of circumstantial evidence. Poehlman expected to contribute to this body of work by demonstrating the change unequivocally in a clinical study of actual patients over time. But when DeNino ran his first analysis, the data did not support the premise.
When Poehlman saw the unexpected results, he took the electronic file home with him. The following week, Poehlman returned the database to DeNino, explained that he had corrected some mistaken entries and asked DeNino to re-run the statistical analysis. Now the trend was clear: HDL appeared to decrease markedly over time, while LDL increased, exactly as they had hypothesized.
Although DeNino trusted his boss implicitly, the change was too great to be explained by a handful of improperly entered numbers, which was all Poehlman claimed to have fixed. DeNino pulled up the original figures and compared them with the ones Poehlman had just given him. In the initial spreadsheet, many patients showed an increase in HDL from the first visit to the second. In the revised sheet, all patients showed a decrease. Astonished, DeNino read through the data again. Sure enough, the only numbers that hadn’t been changed were the ones that supported his hypothesis.
Poehlman brushed DeNino's concerns aside, so DeNino started asking around and other graduate students and postdocs had similar concerns. He got some cautionary advice from a former postdoctoral fellow
Being associated with either falsified data or a frivolous allegation against a scientist as prominent as Poehlman could end DeNino’s career before it even began.
and a faculty member who shared lab space with Poehlman who advised
If you’re going to do something, make sure you really have the evidence.
So DeNino started looking for the evidence.
DeNino spent the next several evenings combing through hundreds of patients’ records in the lab and university hospital, trying to verify the data contained in Poehlman’s spreadsheets. Each night was worse than the one before. He discovered not only reversed data points, but also figures for measurements that had never been taken and even patients who appeared not to exist at all.
DeNino presented his evidence to the university counsel and the response of Poehlman (to his department chair, Burton Sobel) was rather startling.
The accused scientist gave him the impression that nothing was wrong and seemed mostly annoyed by all the fuss. In his written response to the allegations, Poehlman suggested that the data had gotten out of hand, accumulating numerous errors because of handling by multiple technicians and postdocs over the years. “I found that noncredible, really, for an investigator of Eric’s experience,” Sobel later told the investigative panel. “There had to be a backup copy that was pure,” Sobel reasoned before the panel. “You would not have postdocs and lab techs in charge of discrepant data sets.” But Poehlman told Sobel that there was no master copy.
At the formal hearing, Poehlman had a different defense.
First, he attributed his mistakes to his own self-proclaimed ineptitude with Excel files. Then, when pressed on how fictitious numbers found their way into the spreadsheet he’d given DeNino, Poehlman laid out his most elaborate explanation yet. He had imputed data — that is, he had derived predicted values for measurements using a complicated statistical model. His intention, he said, was to look at hypothetical outcomes that he would later compare to the actual results. He insisted that he never meant for DeNino to analyze the imputed values and had given him the spreadsheet by mistake.
The New York Times article points out how pathetic this attempted explanation was.
Although data can be imputed legitimately in some disciplines, it is generally frowned upon in clinical research, and this explanation came across as hollow and suspicious, especially since Poehlman appeared to have no idea how imputation was done.
A large portion of the article examines how research fraud can occur in a system that is supposed to be self-correcting.
First, the people who are mostly likely to notice fraud are junior investigators who are subordinate to their research mentor. It's psychologically and emotionally difficult to confront someone who has devoted time to your professional development. Even when an investigator is emotionally willing to confront their mentor, they have their career concerns to worry about.
The principal investigator in a lab has the power to jump-start careers. By writing papers with graduate students and postdocs and using connections to help obtain fellowships and appointments, senior scientists can help their lab workers secure coveted tenure-track jobs. They can also do damage by withholding this support.
Every university will have a system in place to investigate claims of fraud. But there are problems here as well.
All universities that receive public money to conduct research are required to have an integrity officer who ensures compliance with federal guidelines. But policing its scientists can be a heavy burden for a university. “It’s your own faculty, and there’s this idea of supporting and nurturing them,” says Ellen Hyman-Browne, a research-compliance officer at the Children’s Hospital of Philadelphia, a teaching hospital. Moreover, investigations cost time and money, and no institution wants to discover something that could cast a shadow on its reputation.
“There are conflicting influences on a university where they are the co-grantor and responsible to other investigators,” says Stephen Kelly, the Justice Department attorney who prosecuted Poehlman. “For the system to work, the university has to be very ethical.”
Poehlman himself was careful and chose areas where fraud would be especially difficult to detect. He specialized in presenting longitudinal data, data that is very expensive to replicate. He also presented research results that confirmed what most researchers had suspected, rather than results that would undermine existing theories of nutrition.
At his sentencing, Poehlman was sentenced to one year and one day in federal prison, making him the first researcher to serve time in jail for research fraud.
“When scientists use their skill and their intelligence and their sophistication and their position of trust to do something which puts people at risk, that is extraordinarily serious,” the judge said. “In one way, this is a final lesson that you are offering.”
Questions
1. Do you have experience with a researcher changing the data values after seeing the initial analysis results? What would make you suspicious of fraud?
2. Is the peer-review system of research self-correcting? What changes could be made to this system?
3. When is imputation legitimate and when is it fraudulent?
Submitted by Steve Simon
Independence for national statistics
A better way to restore faith in official statistics, John Kay, Financial Times 25 July 2006.
John Kay, a columnist for the Financial Times, outlines the measures needed to ensure that national statistics are truly independent.
The current state of UK official statistics was covered in a previous Chance article Pick a number, any number, in Chance News 9. That article summarised a report on this topic, to which professional users, such the Royal Statistical Society, gave a cautious welcome to the government’s announcement of independence for the UK Office of National Statistics (ONS).
Kay's article follows up on the reaction to that report. He tells us that accurate public information is a prerequisite of democracy, government statisticians are honest people but ministers (politicians) needs are often for propaganda rather than facts. Kay claims that decentralisation of responsibility for the production of official statistics has created a two-tier system in the UK.
statistics produced by the Office for National Statistics (ONS), which operates to internationally agreed criteria, are of higher quality than those produced by (government) departments.
The proposal to hand responsibility for all official statistics to the ONS was rejected, as were the suggestions for greater independence, made by bodies such as the Statistics Commission and the Royal Statistical Society,
- separating statistical information from political statements,
- reducing access by ministers to new data before their release,
- giving parliament a defined role in the appointment of the National Statistician.
Instead, the latest news is that the ONS will be demoted to a non-ministerial department. The worst news is the abolition of the Statistics Commission, which reviews all government statistics, and has made itself unpopular with government by proving itself robustly independent.
Kay also cautions that statistics may be misused in contexts other than those intended. The value of health services increases as incomes rise and it can be argued that this increases the value of health output even if outcomes and procedures are unchanged. This statistical adjustment provides no basis whatever for claims that the National Health Service is more efficient. But the assertion grabs a headline, and it is only much later that pedantic journalists and academics can discover what is actually going on.
Submitted by John Gavin.
An example of Simpson's Paradox
Study finds wealth inequality is widening worldwide
New York Times, Dec. 6, 2006, C-3
by Eduardo PorterThe article contains stats from a 2000 report on wealth distribution by country and worldwide. The article points out (toward the end) that even though every country has seen growing income inequality in the last six years, the *worldwide* inequality gap may be narrowing from the year 2000 stats to the present. The reason is the huge growth and wealth accumulation in China and India, which raises income overall, even though both those countries have also seen greater inequality.
Submitted by Bob Dobrow
Predecessors of Poehlman
Steve Simon's post, "I wasn't making up data, I was imputing!" is quite interesting and informative. Nevertheless, some elaboration is in order regarding fraud and Simon's statement that "The Poehlman scandal represents perhaps the biggest case of research fraud in recent history."
The term "recent history" is sufficiently elastic to permit quoting myself in the 1980s:
Admittedly Slutsky is an extreme example...even after the investigation [proving fraud in many of his papers]...Robert G. Slutsky was [still] given credit for [an additional] 77 publications in his seven years with [the University of California, San Diego]...in 1984 he published at the astonishing rate of one paper every ten days..Slutsky's phenomenal productivity was encouraged, applauded and rewarded...John R. Darsee [another cardiologist but at Harvard], had about 100 papers in a period of two years and his undoing in 1981 was colleagues who secretly saw him forging the data.
Put Slutsky and Darsee into Google.com and you will see the entire treatment. My point is that the Eric Poehlman scandal is nowhere near the biggest--Slutsky and Darsee involved entire prestigious labs. And we tend to ignore history at our peril. An extensive treatment of Slutsky, Darsee and many others (Baltimore, Imanishi-Kari, Spector, Summerlin, Long, Alsabti, Soman, Breuning, Pearce, Hermann, Brach, Schoen, not to mention more illustrative predecessors such as Newton, Mendel, Pasteur and Freud) can be found in The Great Betrayal: Fraud in Science by Horace Freeland Judson [Harcourt, Inc., 2004].
Although Judson's book is a wonderful page-turner, go to www.bmj.com/cgi/content/full/329/7471/922 to see a critique of the book by Peter Wilmshurst, a British cardiologist who is very active in unearthing medical fraud. Wilmshurst suggests that "Judson paints a rosier picture of the mechanisms for dealing with research fraud than I recognize." Further, "Judson only briefly describes what may be the most common form of research misconduct: failure to publish results...for the sake of company profits."
Although research frauds tend to have things in common--colossal egos, external as well as internal pressures, desire for fame, money, etc.--each instance is possibly unique. Poehlman evidenced a typical trait: he fabricated the data. According to the original New York Times article, his study on menopause "was almost entirely fabricated. Poehlman had tested only 2 women, not 35." On the other hand, Poehlman was downright stupid to have changed his (real, existing) cholesterol data to fit his (and others) belief that cholesterol levels worsen with age because he had the only large longitudinal study, implying that it would be publishable and valuable regardless of the results. The other unusual feature was that "He was only the second scientist in the United States to face criminal prosecution for falsifying research data."
Buried in the NYT article is the statement made by Steven Heymsfield, an obesity researcher at Merck and should be a guiding light for all researchers: "But deans love people who bring in money and recognition to universities, so there is Eric."
Discussion
1. Use a search engine to determine what fraud was committed by some of the predecessors of Poehlman.
2. Scientists claim that peer review and duplication of results act to inhibit fraud. Pick a researcher and determine why either or both failed.
3. This wiki ends with a disparaging remark about university deans. Defend them.
Submitted by Paul Alper
Wealth of nations
- Winner takes (almost) all, The Economist, 9th Dec 2006.
- Pioneering study shows richest 2 percent own half world wealth, James Davies of the University of Western Ontario, Anthony Shorrocks and Susanna Sandstrom of UNU-WIDER and Edward Wolff of New York University.
The Helsinki-based World Institute for Development Economics Research of the United Nations University (UNU-WIDER) has conducted what it claims is a path-breaking study into the most comprehensive study of personal wealth ever undertaken: it is the first-of-its-kind to cover all countries in the world and all major components of household wealth, including financial assets and debts, land, buildings and other tangible property.
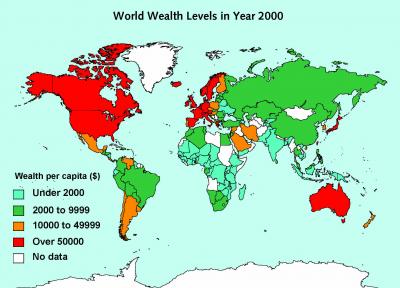 World Wealth Levels in Year 2000: The world map shows per capita wealth of different countries. Average wealth amounted to $144,000 per person in the USA in year 2000, and $181,000 in Japan. Lower down among countries with wealth data are India, with per capita assets of $1,100, and Indonesia with $1,400 per capita. Source: UNU-WIDER.
World Wealth Levels in Year 2000: The world map shows per capita wealth of different countries. Average wealth amounted to $144,000 per person in the USA in year 2000, and $181,000 in Japan. Lower down among countries with wealth data are India, with per capita assets of $1,100, and Indonesia with $1,400 per capita. Source: UNU-WIDER.The report contains a plethora of statistics, such as:
- The richest 2% of adults in the world own more than half of global household wealth.
- The richest 1% of adults alone owned 40% of global assets in the year 2000.
- The richest 10% of adults accounted for 85% of the world total.
- The bottom half of the world adult population owned barely 1% of global wealth.
- To be among the richest 10% of adults in the world required $61,000 in assets.
- More than $500,000 was needed to belong to the richest 1% (37 million members).
- Household wealth amounted to $125 trillion in the year 2000, equivalent to roughly three times the value of total global production (GDP) or to $20,500 per person. Adjusting for differences in the cost-of-living across nations raises the value of wealth to $26,000 per capita when measured in terms of purchasing power parity dollars.
- Wealth levels vary widely across countries: ranging from $37,000 per person for New Zealand and $70,000 for Denmark to $127,000 for the UK (for high-income OECD nations).
- North America has only 6% of the world adult population, yet it accounts for 34% of household wealth.
- Wealth is more unequally distributed than income across countries. High income countries tend to have a bigger share of world wealth than of world GDP. The reverse is true of middle- and low-income nations.
The authors warn about the ambiguity in the definition of wealth
One should be clear about what is meant by 'wealth'. In everyday conversation the term 'wealth' often signifies little more than 'money income'. On other occasions economists use 'wealth' to refer to the value of all household resources, including human capabilities.
The authors define wealth to mean 'the value of physical and financial assets less debts', so wealth represents the ownership of capital. They claim that capital is widely believed to have a disproportionate impact on household well-being and economic success, and more broadly on economic development and growth.
The authors use the Gini value to measure inequality on a scale from zero to one. They claim that wealth is shared much less equitably than income. Income inequality ranges from 35% to 45% and wealth inequality are usually between 65% and 75% (e.g. zero would mean everyone has the same income and one means that one person has all the income and everyone else has none). The authors claim
The global wealth Gini for adults is 89%. The same degree of inequality would be obtained if one person in a group of ten takes 99% of the total pie and the other nine share the remaining 1%.
Surprisingly, household debt is seen as relatively unimportant in poor countries. As the authors of the study point out:
while many poor people in poor countries are in debt, their debts are relatively small in total. This is mainly due to the absence of financial institutions that allow households to incur large mortgage and consumer debts, as is increasingly the situation in rich countries. Many people in high-income countries have negative net worth and—somewhat paradoxically—are among the poorest people in the world in terms of household wealth.
For example, the bottom half of the Swedish population have a collective net worth of less than zero, although Nordic countries, in general, seem to thrive with relatively little personal wealth.
Questions
- A presentation format consisting of a list of such point-estimate statistics seems disjointed, as it swaps repeatedly between statistics for the richest and the poorest. Could the data be more meaningfully presented via a distribution?
- The graph shows a discrete five point distribution. Is such a split of the data into buckets such as 'under 2000' and 'over 50000' meaningful?
- Mapping the output to countries via colours, shows the geographic distribution of the underlying variable, wealth. What is misleading about this graph? How might countries be scaled in size to better relflect the data.
- How might switching from measuring wealth to income affect the preception of the results? (A gini measure of income inequality is available from Wikipedia, along with time trends since the 1940s.)
- Two high wealth economies, Japan and the United States, show very different patterns of wealth inequality, with Japan having a wealth Gini of 55% and the USA a wealth Gini of around 80%. Speculate on what factors might explain this difference.
Submitted by John Gavin.
Science in the Courtroom
When questions of science come to a courtroom, truth has many faces
New York Times, 5 December 2006, F3
Cornelia DeanThis article appeared as the US Supreme Court began hearing its first case involving global warming. A case has been filed against the federal government by a group of state and local governments, together with environmental groups. These plaintiffs charge that that the Environmental Protection Agency, by refusing to regulate greenhouse gas emissions, is failing to enforce the Clean Air Act.
Some of the arguments involve legal technicalities, such as whether the states actually have standing to bring such a suit. But the present article is concerned with the scientific evidence, and what responsibility the Court has to educate itself about the scientific underpinnings of a case. The article draws the following distinction between statistical and legal standards for proof:
Typically, scientists don't accept a finding unless, statistically, the odds are less than 1 in 20 that it occurred by chance. This standard is higher than the typical standard of proof in civil trials ("preponderance of the evidence") and lower than the standard for criminal trials ("beyond a reasonable doubt").
The article provides some historical references on how the Court has previously viewed scientific testimony, beginning with discussion of the 1923 Frey case on lie detectors, which introduced the "general acceptance" standard. This was updated in the 1993 case Daubert v. Merrell Dow Pharmaceuticals, which involved the drug Bendectin and its possible association with birth defects. The Court introduced the concepts of "testability" and "peer review" into its deliberations on science. In the 1998 case General Electric Company v. Joiner, the Court ruled that "judges could reject evidence if there was simply too great a gap between 'the data and the opinion proffered.'"
The main thrust of the article, however, is that the Court still has been too slow to keep up with the explosion of scientific knowledge, which can be expected to play an ever larger role in future cases. For example, when corrected on a technical point in the discussion about carbon dioxide, Justice Scalia responded, "Troposphere, whatever. I told you before I'm not a scientist."
DISCUSSION QUESTIONS
(1) What do you think of the suggested correspondence between the legal and statistical standards for evidence? What probability numbers would you attach to "preponderance of the evidence" and "beyond a reasonable doubt"?
(2) How should a judge decide when there is too great a gap between "the data and the opinion proffered"?
Submitted by Bill Peterson
Magic numbers
Technical failure, Buttonwood, The Economist, Sep 21st 2006.
In financial markets, some traders believe that markets change trend when they reach, say, 61.8% of their previous high, or 61.8% above their low. Such seemingly magical numbers are derived from Fibonacci series and are often given special names such as the golden ratio (approx 1.618) in architecture and design.
This article categorises such traders as follows:
Believers in Fibonacci numbers are part of a school known as technical analysis, or chartism, which believes the future movement of asset prices can be divined from past data. Some chartists follow patterns such as head and shoulders and double tops; others focus on moving averages; a third group believes markets move in pre-determined waves. The Fibonacci fans fall into this last set.
The Economist article points out that a new study, by Professor Roy Batchelor and Richard Ramyar of the Cass Business School, finds no indication that trends reverse at the 61.8% level, or indeed at any predictable milestone in American stockmarkets.
Fibonacci numbers at least have the virtue of creating a testable proposition; one that they appear to fail. However, chartists will not be completely discouraged as The Economist highlights another study which claims that 58 of 92 modern studies of technical analysis produced positive results. The authors of this second paper conclude:
Despite the positive evidence ... it appears that most empirical studies are subject to various problems in their testing procedures, e.g. data snooping, ex-post selection of trading rules or search technologies and difficulties in estimation of risk and transaction costs.
The Economist article goes on to imply that the theory which dominates at any point in time may simply be a matter of fashion:
If financial markets are efficient, technical analysis should not work at all; the prevailing market price should reflect all information, including past price movements. However, academic fashion has moved in favour of behavioural finance, which suggests that investors may not be completely rational and that their psychological biases could cause prices to deviate from their 'correct' level.
The article claims that chartism probably works best in the foreign-exchange market because major participants, especially central banks, are not 'profit-maximising' leading to inefficient pricing. Furthermore, some technical predictions may be self-fulfilling; if everyone believes that the dollar will rebound at 100 yen, they will buy it as it approaches that level.
But it finishes with a warning
Chartists fall prey to their own behavioural flaw, finding “confirmation” of patterns everywhere, as if they were reading clouds in their coffee futures.
Questions
- Can you think of possible ways to alleviate the biases mentioned: 'data snooping', 'ex-post selection of trading rules' and 'transaction costs'? Which of these issues do you think is easiest to incorporate into an analysis?
- (from Wikipedia) 'Critics of technical analysis include well known fundamental analysts. Warren Buffett has said, I realized technical analysis didn't work when I turned the charts upside down and didn't get a different answer and if past history was all there was to the game, the richest people would be librarians.' How might you test if Buffett's assertions are true?
- (from Wikipedia) 'To a technician, however, Buffett paraphrased [technical analysis] when he commented in a recent conference on investing in mining companies, in metals and oils, there's been a terrific [price] move. It's like most trends: at the beginning, it's driven by fundamentals, then speculation takes over ... then the speculation becomes dominant.' Do you agree that Buffett is acknowledging that markets are inefficient because they trend? Would a basic, first-order, auto-regressive model (AR(1)) on price differences be sufficient to test the existance of such a trend?
- Technicians argue that many investors base their future expectations on past earnings, track records, etc. Because future stock prices can be strongly influenced by investor expectations, technicians claim this means that past prices can influence future prices. Does this argument persuade you?
Further reading
- Magic numbers in the Dow, Roy Batchelor and Richard Ramyar, Cass Business School, City of London, Sep 2006.
- The Profitability of Technical Analysis: a review, by Cheol-Ho Park and Scott H Irwin, University of Illinois, October 2004.
- The random walk hypothesis is at odds with technical analysis and charting. This hypothesis claims that stock price movements are a Brownian Motion with either independent or uncorrelated increments. In such a model, movements in stock prices are not dependent on past stock prices, so trends cannot exist and technical analysis has no basis. Random Walk advocates such as John Allen Paulos believe that technical analysis and fundamental analysis are pseudo-sciences. The latter tried his hand at playing the stock markets without success:
A Mathematician Plays the Stock Market is the story of my disastrous love affair with WorldCom, but lest you dread a cloyingly personal account of how I lost my shirt (or at least had my sleeves shortened), I assure you that the book's primary purpose is to lay out, elucidate, and explore the basic conceptual mathematics of the market. I'll examine ... issues associated with the market. Is it efficient? random? Is there anything to technical analysis, fundamental analysis, and other supposedly time-tested methods of picking stocks? How can one quantify risk? What is the role of cognitive illusion and pyschological foible (to which, alas, I am not immune)? ... In short, what can the tools of mathematics can tell us about the vagaries of the stock market?
Submitted by John Gavin.