Chance News 14
Quotation
The [Supreme] Court concluded that mental health professionals' predictions were "not always wrong...only most of the time."
Forsooth
In theory, if you were to buy 50 tickets and your neighbor bought one, neither of you would have a better or worse chance of winning, We like to say it only takes one ticket to win."
in a discussion of the record Powerball jackpot of 360 million dollars.
Gerd Gigerenzer's Calculated Risks Revisited
Chance News 11.03 had a lengthy and very positive review of Gerd Gigerenzer's book Calculated Risks: How To Know When Numbers Deceive You. Readers are urged to download that excellent review because of the information contained. However, the book is so good and so persuasive that it is worth another look in order to alert readers to some other aspects of the book and how it relates to subsequent events.
The aforementioned review did not mention the abundant number of actual, real-world incidents cited in which doctors, lawyers and social workers, not to mention patients, clients and jurors, were unable to unscramble the difference between P(X| Y) and P(Y| X). Also not mentioned was Gigerenzer's dim view of screening for breast cancer and prostate cancer. Screening may be defined, according to H. Gilbert Welch, as "the systematic examination of asymptomatic people to detect and treat disease." See Chance News 12 for a review of Welch's 2004 book Should I Be Tested For Cancer? Maybe Not And Here's Why. Welch echoes and amplifies Gigerenzer contention that (mass) screening is counterproductive, especially when there is little evidence that a cure exists. Just to complicate matters, however, see "Mammograms validated as key in cancer fight" in Chance News 8 which indicates that mammography screening does reduce the death rate of breast cancer, . Unfortunately, the article in the New England Journal of Medicine referred to does not explain why mammogram screening is deemed responsible for 28 to 65% of the 24% drop in the breast cancer death rate. Gigerenzer would prefer, and this is one of his main points, that any statistical data be given in counts rather than in percentages, especially percentages without a base rate, such as relative risk which he views as the most misleading.
| Treatment | Deaths per 1000 women |
|---|---|
| No mammography screening | 4 |
| Mammography screening | 3 |
Consequently, there is "a 25 percent relative risk reduction." He would prefer focusing on the difference in the number of deaths which yields the more revealing and perhaps more honest statement: "The absolute risk reduction is 4 minus 3, that is, 1 out of 1000 women (which corresponds to .1 percent)." However, "Counting on their clients' innumeracy, organizations that want to impress upon clients the benefits of treatment generally report them in terms of relative risk reduction...applicants [for grants] often feel compelled to report relative risk reductions because they sound more impressive." Although he did not use this example, one's relative "risk" of winning the lottery is infinitely greater if one buys a ticket, yet one's absolute "risk" of winning has hardly improved at all.
Most of his numerical examples are typified by his discussion of the cartoon given below
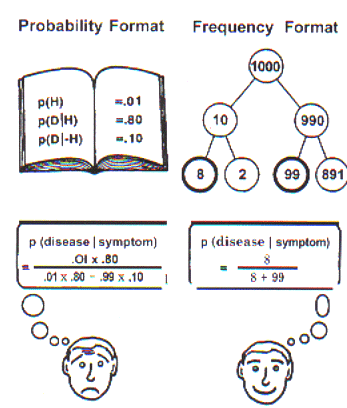
which indicates the superiority of dealing with counts. Note that "H" represents having the disease and "D" represents a diagnosis having the symptom as seen by testing positive. Characteristically, there is a large number in the population who do not have the disease and because of the possibility of a wrong classification, the number of false positives (99) outweighs the number of true positives (8) resulting in P(disease| symptom) being much lower (8/(8+99)) than P(symptom| disease) (.8). This type of result, low probability of disease given symptom, is true even when ".8" is replaced by a number much closer to 1 provided there are many more who do not have the disease.
Here is an example he did not consider but it also illustrates the superiority of dealing with counts. Instead of two populations--diseased and healthy--which are greatly different in size, consider Boys and Girls and the desire to predict gender based on some simple test. Assume that 50% of births are Boys so that P(Boy) = P(Girl) = 1/2. A simple, inexpensive, non-invasive gender-testing procedure indicates that it is "perfect" for boys, P(Test Boy| Boy) = 1, implying P(Test Girl| Boy) = 0. Unfortunately, this simple, inexpensive, non-invasive gender-testing procedure for girls is a "coin toss," P(Test Girl| Girl) = P(Test Boy| Girl) = 1/2. Application of Bayes theorem yields what seems to be a strange inversion, P(Boy| Test Boy) = 2/3 and P(Girl| Test Girl) = 1. That is, somehow, "perfection" switched from Boy to Girl. The test is perfect in "confirming" that a Boy is a Boy and has a 50% error rate in confirming that a Girl is a Girl. The test is perfect in "predicting" that a person who tests as a girl is in fact a girl but has 33% error rate in predicting that a person who tests as a Boy is in fact a Boy. Thus, the term perfect is ambiguous. Perfection in confirmation, i.e., the test conditional on the gender, does not mean perfection in prediction, i.e., the gender conditional on the test.
Some of the puzzlement disappears if we deal with counts; the table below is equivalent to Gigerenzer's "tree" diagram. Assume 50 Boys and 50 Girls to start with. Every one of the 50 Boys will test as a Boy--none of the Boys test as a Girl; of the 50 Girls, 25 will test as a Boy and 25 will test as a girl. Therefore, P(Girl| Test Girl) = 1. One is tempted to to explain the switch by using the lingo of medical testing: false positives, false negatives, sensitivity, specificity, positive predictive value, negative predictive value. However, one hesitates to designate either gender as diseased even though the mathematics is the same.
| Test Boy | Test Girl | Total | |
|---|---|---|---|
| Boy | 50 | 0 | 50 |
| Girl | 25 | 25 | 50 |
Gigerenzer rightly concludes that the language of statistics is not natural for most individuals. Perhaps the puzzlement in this specific example is at least partly due to the natural language known as English. Boys, Girls, Test Boys and Test Girls are too confusing. . Replace "Boy" by "Norwegian" and "Girl" by "German" and assume that there are as many Norwegians as Germans. Let every Norwegian be "Blond," so that P(Blond| Norwegian) = 1 and only half the Germans are Blond. Thus, P(German| Not Blond) =1; the switch, P(German| Not Blond) = P(Blond| Norwegian) = 1, is rather obvious. Is the this situation easier to understand because of the linguistics--hair color and ethnicity are easily distinct as Test Boy and Boy are not?
DISCUSSION QUESTIONS
1. Gigerenzer has a chapter entitled, "(Un)Informed Consent." Based on your experience, what do you imagine the chapter contains?
2. A drawing of two tables (that is, physical tables on which things are placed) appears on page 10. He claims the tables (due to Roger Shepard) are identical in size and shape. After staring at them in disbelief of the claim, how would you verify the contention?
3. Physicians sometime make the following type of statement:"Never mind the statistics, I treat every patient as an individual." Defend this assertion. Criticize this assertion.
4. The physicist, Lord Rutherford, is reputed to have said, " If your experiment, needs statistics you ought to have done a better experiment." Defend and criticize Lord Rutherford.
5. Assume an asymptomatic woman has a mammogram which looks suspicious and then a biopsy which is negative. Would she be grateful for the clean bill of health or would she become an advocate who opposes (mass) screening? Suppose instead we assume a man has a suspiciously high PSA and the painful multiple biopsies (6-12 "sticks") are all negative. Would he be grateful for the clean bill of health or would he become an advocate who opposes (mass) screening?
6. Calculated Risks also deals with the risk to the physician making a recommendation and a diagnosis. Discuss why in our present-day litigious society the risks to the physician (who may or may not recommend a test or may or may not make a diagnosis) are not symmetrical. Along these lines, who are the vested interests involved in maintaining screening and testing?
7. Revisit the Boy/Girl scenario but now the test always says Boy regardless of gender, P(Test Boy| Boy) = P(Test Boy| Girl) = 1. Complete the table for this version. Obviously, this test has the advantage of being extremely simple, cost-free and non-invasive. Use either the Probability Format or the Frequency Format to comment on the statistical worthiness of this test.
Submitted by Paul Alper
Two more medical studies conflicting with previous studies
Low-fat diet does not cut health risks, Study finds
New York Times, Feb. 8, 2006
Gina Kolata
Cutting fat alone isn't enough, women advised
USA TODAY, Feb, 7, 2006
Rita Rubin
Popular herb shows no benefit for prostate
Wall street journal, Feb. 9, 2006
Syllvia Pagan Westphal
In the New York Times article we read:
The largest study ever to ask whether a low-fat diet reduces the risk of getting cancer or heart disease has found that the diet has no effect.
The $415 million federal study involved nearly 49,000 women ages 50 to 79 who were followed for eight years. In the end, those assigned to a low-fat diet had the same rates of breast cancer, colon cancer, heart attacks and strokes as those who ate whatever they pleased, researchers are reporting today.
In the Wall Street Journal article we read:
Saw palmetto, an herbal supplement taken by 2.5 million Americans for problems with enlargement of the prostate gland, is no more effective than a placebo in alleviating the condition, according to a new study
The perception that saw palmetto works had been supported by a number of clinical trials over the years. A comprehensive 2002 analysis of 21 trials involving over 3,000 men found that studies credited saw palmetto with providing "mild to moderate improvement in symptoms with fewer adverse events than finasteride (approved by the Food and Drug Administration to treat benign enlargement).
The saw palmetto study was reported in the New England Journal of Medicine February 9, 2006 and the low-fat diet study was reported in Jama, February 8, 2006.
The saw palmetto study had 225 participants randomized to give 112 saw palmetto and 113 placebo and the study lasted from July 2001 to May 2003.
So once more the general public will wonder what the truth is. Commenting on the diet study Berkeley statistician David Freedmn is quoted as saying that the studies were well designed and should be taken seriously.
Two of the 32 authors of the study, Judith Hsia, professor of medicine at George Washington University in Washington, D.C. and Ross Prentice, professor of biostatistics at the University of Washington in Seattle, were interviewed by Ira Flato on NPR's Talk of the Nation Friday Science program February 10, 2006. You can listen to them trying to do damage control here . The say that women should certainly not quit trying to control their diet. They point out that the study did not distinquish between "good" and "bad" fats. Prentice remarks that the incidence rate of breast cancer was 9% less in control group than in the placebo group. When Ira remarks that the study said that the difference was not significant, Prentice replied that you have to understand what statistical signficance meant and adds that if it were 10% it would have been signficant.
The authors of the paper also comment that the study was not able to continue for the length of time originally planned and since the trend for the incidence of Breast cancer was in the right direction so it is possible that the difference might be significant over the longer time. Here is a graphic from the Jama article that shows the difference in the incident rates over time http://www.dartmouth.edu/~chance/chance_news/for_chance_news/wiki/diet.png .
Further reading
The low-fat diet study has attracted a lot of attention from bloggers.
- Man Bites Dog and Man Bites Dog II, Michael R. Eades, M.D. offers a critical review of the design of the study.
- Regina Wilshire's blog on why we don't need more time and/or more studies to 'prove' that low-fat dieting really works.
- Gina Kolata writes in Science Times February 14 a sequel to her February 8th article. You will also find here her answers to readers who questioned the validity of the study.
- Women's health sudies leaves questions in place of certainty.Denise Grady, New York Times, Feb. 19. This article begins with/
So what do women do now? The results of two major studies over the past two weeks have questioned the value of two widely recommended measures: calcium pills and vitamin D to prevent broken bones, and low-fat diets to ward off heart disease and breast and colon cancer.
The article discusses the conflicts between statisticians and researchers who want to look at subgroups to try to argue that despite the lack of significance one can see hopeful signs. Statistician Susan Ellenberg remarks:
The probability that you will see a spuriously positive effect gets very big very quickly.
She quotes another statistician, Richard Peto of Oxford University, who said of subgroups:
You should always do them but you should never believe them
You will also find in this article a nice graphic summerizing the results of the Women's study.
A day in the life of a human rights statistician
Coders Bare Invasion Death Count, By Ann Harrison, Wired News, 9-Feb-06.
How statistics caught Indonesia's war-criminals , Cory Doctorow, BoingBoing.net
A group of determined programmers and statisticians, the Human Rights Data Analysis Group, released a report documenting over civilian deaths in the former Portuguese colony, which occurred from a year prior to the Indonesian army's invasion in 1975, to the country's 1999 independence referendum that formally ended the occupation. Statistical analysis establishes that at least 102,800 (+/- 11,000) Timorese died as a result of the conflict. Approximately 18,600 (+/- 1000) Timorese were killed or disappeared, while the remainder died due to hunger and illness in excess of what would be expected due to peacetime mortality.
Group director Patrick Ball says
By having an accurate statistical picture of the suffering, we can draw conclusions about what the causes of the violence might have been and identify likely perpetrators with a claim based on thousands of witnesses.
The group established three datasets that integrated quantitative methods into broader truth seeking activities. These datasets included:
- The commission's statement-taking process, which collected almost 8,000 narrative testimonies from people in every sub-district;
- A census of all public graveyards in the country (encompassing approximately 319,000 gravestones);
- A retrospective mortality survey drawing on a probability sample of approximately 1,400 households throughout the thirteen districts of Timor-Leste.
In establishing these data, HRDAG and the Commission for Reception, Truth and Reconciliation in East Timor (CAVR) pioneered a number of new techniques and methods. No other truth commission has ever undertaken a retrospective mortality survey. While gravestone information for mortality estimation has been used by historical demographers for mortality estimations, this is the first time that a human rights project has employed such methods. These projects were so large that HRDAG developed automated techniques to link multiple reports of the same death - a key component of multiple systems estimation, a technique that uses two separately collected but incomplete lists of a population to estimate the total population size.
HRDAG uses the multiple systems estimation technique in human rights cases to project the total number of violations, including those that were never documented. This information is vital to producing a complete accurate historical record of the violations and to provide evidence at the trial of the architects of large-scale human rights abuses. In order to make statistical inferences from multiple systems estimation, it is necessary to:
- Identify overlapping reports
- Control for bias and variation in coverage rates
- Estimate the total magnitude
Ball has spent the last 15 years building systems and conducting qualitative analysis for large-scale human rights data projects around the world. HRGAD researchers used comparative analysis of the datasets to uncover patterns of deaths and build objective evidence of abuses. The team also developed an array of descriptive statistical analysis profiling the scale, pattern and structure of torture, ill-treatment, arbitrary detention and sexual violations. In order to estimate what was missing from the data, the HRDAG developed software to link multiple reports of the same death in a technique called record linkage. They then used multiple systems estimation to calculate the number of deaths that no one remembered.
Romesh Silva, a HRDAG field statistician who led the design and implementation of the project's data, says
The Indonesian military has persistently argued that excess mortality in Timor due to its occupation of Timor was zero. This claim can now be tested empirically and transparently with the tools of science instead of merely being debated with the tools of political rhetoric.
The final report of the CAVR was handed over to the President of Timor-Leste on 31 October 2005. The President of Timor-Leste then tabled the report at a special sitting of Timor-Leste's National Parliament on 28 November, 2005 - which coincided with the 30th anniversary celebrations of Timor's Proclamation of Independence.
Further reading
- The Human Rights Data Analysis Group (HRDAG) develops information technology solutions and statistical techniques to help human rights advocates build evidence-based arguments.] See the FAQ for more info.
- The Profile of Human Rights Violations in Timor-Leste, 1974-1999. A Report by the Benetech Human Rights Data Analysis Group to the Commission on Reception, Truth and Reconciliation of Timor-Leste. 9 February 2006.
- Romesh Silva and Patrick Ball designed and conducted the statistical analysis and wrote this report. Their on-line profiles provide more information about their statistical work and the awards that they have received. The are also profiles of other statistical consultants at HRDAG.
Two short papers by Romesh and Ball are worth reading:
- The Demography of Large-Scale Human Rights Atrocities: Integrating demographic and statistical analysis into post-conflict historical clarification in Timor-Leste. Romesh Silva and Patrick Ball. A 5-page paper presented at the 2006 meetings of the Population Association of America.
- My brilliant career - Quantitative Data Analysis and Large-Scale Human Rights Violations: An Example of Applied Statistics at the Grassroots. Romesh Silva. Gazette of the Australian Mathematical Society. Canberra (Australia). Volume 32, Number 2, May 2005. A 5-page paper on where a mathematics education can lead you.
- "in the late 1990’s as I was completing my honors degree in statistics at UNSW, I became increasingly involved with Amnesty International ... I began to wonder how I might be able to directly apply my mathematical education and quantitative skills to international human rights. ... As the field of human rights statistics is relatively new, our main challenge remains in attracting more mathematicians and statisticians to work in this area and also communicating to the human rights field how quantitative data analysis can contribute to accountability and truthtelling processes."
Submitted by John Gavin.
Another record jackpot for the Powerball lottery
Europe's statisticians are too gloomy
A numbers racket, The Economist, 18-Feb-06.
This article highlights how statistical biases can influence perceptions of economic growth.
Since the start of European Monetary Union in 1999, revisions to gross domestic product (GDP) growth have almost always been upwards. In contrast, revisions in America have tended to be downwards. The initial figures which grab newspaper headlines therefore exaggerate Europe's economic underperformance.
The Economist resists the obvious conclusion:
Discounting the obvious explanation that American statisticians are born optimists, it is unclear what lies behind the consistent direction of these revisions.
This article is based on a paper by Kevin Daly, an economist at Goldman Sachs. He calculates that, based on the GDP-growth figures first published in each quarter, the euro area would have grown by an annual average of only 1.6% in the six years to 2004. Yet the latest figures put the growth rate at 2.0%. In contrast, the first published figures gave America an average growth rate of 3.1%; but that has now been shaved down to 2.8%. The revisions have cut the reported gap between growth rates in America and the euro area in half. As a result, the euro area's GDP per head has in fact grown at the same pace as America's.
The Economist goes on to comment:
Europe could rejoice in further upward revisions to growth if its governments were to adopt American statistical practices. Price deflators there take more account of improvements in the quality of goods, such as computers, and thus a given rise in nominal spending implies faster growth in real terms. By using higher inflation rates, the euro area understates its growth relative to America's. In addition, American statisticians consider firms' spending on software that is written in-house to be investment, while in the euro area it is often counted as an expense and so is excluded from final output. The surge in software spending has therefore inflated America's relative growth.
On past experience, Europe's statisticians should add half a percentage point to their first guesses of GDP growth. By also switching to American practices, they could boost growth even further. Instead, their cautious ways are making Europe's economies look more dismal than they are, and gloomy headlines are discouraging consumers from spending. Perhaps Europe should outsource the compilation of its statistics to America, and then watch the boom.
Further reading
Has Euroland Performed That Badly?, Kevin Daly, Golman Sachs. Daly says
Euroland productivity when measured appropriately is not only close to US levels but, over the past ten years as a whole, its growth has continued to surpass that of the US. The US’s superior GDP performance over this period has not been attributable to faster productivity growth but to a more rapidly expanding labour force that is prepared to work longer hours.
Submitted by John Gavin.