Chance News 28

Forsooth

The following Forsooth is from the June 2007 RSS News.

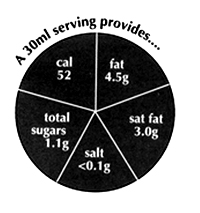
from label for `Crème fraîche' (Sainsbury's)
2006

This is less of a Forsooth if you see how the Wheel of Health is described on Sandbury's website.

Sainsbury’s traffic-light labeling on the front of food and drink tells you if it has high (red), medium (amber) or low (green) amounts of fat, saturated fat, salt, sugar and calories.

http://www.dartmouth.edu/~chance/forwiki/SainsburyColor.jpg

Does social rank determine IQ?

Big Brothers Are Smarter Than Younger Ones, Kate Shellnutt, Bloomberg.
Families' Eldest Boys Do Best on Tests, Randolph E. Schmid, AP Science Writer, FoxNews, 21 June, 2007.
To the First-Born Go the Smarts, Steven Reinberg, HealthDay.
Research Finds Firstborns Gain the Higher I.Q., Bendict Carey, NY Times, 22 June 2007.

Older brothers are smarter than their younger siblings but it is predominantly their social rank in the family, rather than their birth order or genetics, that is the cause according to a recent paper in the two journals: Science and Intelligence, led by Petter Kristensen, a doctor at Norway's National Institute of Occupational Health, in Oslo.

Most large birth-order studies are across-family, comparing the IQs of all oldest siblings surveyed to those of all youngest siblings surveyed. But such results have been criticized for failing to take account of the differences in upbringing between families. This large-scale, within-family study attempts to settle more than a half-century of scientific debate about the relationship between I.Q. and birth order. (With such lofty claims being made and because we have previously discussed this topic in Chance News - The more the merrier? First born do better at school, this Chance News article is rather long.)

Researchers have long had evidence that firstborns tended to be more dutiful and cautious than their siblings, and some previous studies found significant I.Q. differences. Until now, no one had a clear explanation for this negative association between birth order and intelligence level. Among competing explanations, two have stood out:

• one emphasizes interactions within the family for intellectual stimulation of the low birth-order siblings
• another cites prenatal or gestational factors.

For example, psychologist Robert Zajonc claims that older siblings consolidate and organize their knowledge in their natural roles as tutors to their junior siblings, knowledge which influences their IQ score. These lessons, in short, benefit the teacher more than the student. Some studies claim that both the older and younger siblings tend to describe the firstborn as more disciplined, responsible, high-achieving. While other studies suggest that, to distinguish themselves, younger siblings often develop other skills, like social charm, to compensate for lower IQ. This might explain evidence that younger siblings often live more adventurous and less conventional lives than their older brother or sister. For example, they are more likely to participate in dangerous sports and are more likely to travel to exotic places.

Some quote the example of Nobel prize winners, firstborns have won more Nobel Prizes in science than younger siblings, but often by advancing current understanding, rather than overturning it, allegedly. In contrast, Charles Darwin was the fifth of six children, Nicolaus Copernicus grew up the youngest of four and René Descartes was the youngest of three.

The authors anticipated that men who had a biological rank different from their social rank, in their family, would score better than males of similar birth order who had not experienced the early loss of elder siblings, if the social interaction hypothesis was right; whereas similar scores would support the gestational hypothesis.

The authors based their findings on the IQs of Norwegian military draftees, as measured at enlistment, and then compared the numbers with those for the draftees' brothers. They had data on birth order, health status and I.Q. scores of a quarter of a million 18 and 19 year old men, in the largest study ever to compare the intellect of children within families. (This study ignores women.) The authors allowed for factors such as parents’ education level, maternal age at birth and family size. But still eldest children scored an average of 103.2, about 3 percent higher than second children (100.3) and 4 percent higher than thirdborns (99.0). The scientists then looked at I.Q. scores in 64,000 pairs of brothers, and found the same results. Differences in household environments could not explain elder siblings’ higher scores.

Three points on an I.Q. test may not sound like much but some experts say it could be the difference between a high B average and a low A, for example. Its cumulative effect could be the difference between admission to an elite private school and a less exclusive public one.

Remarkably, the paper also claims that when an older brother dies, the next-oldest one scores better on subsequent tests. So it is family dynamics, not biological factors like prenatal environment, that are the critical factor. Birth order made no difference after accounting for social order

Conscripts of first rank in social terms, no matter their biological rank, scored equal to firstborn men

To test whether the difference could be due to biological factors, the researchers examined the scores of young men who became the eldest in the household after an older sibling had died. Their scores came out the same, on average, as those of biological firstborns.

This is quite firm evidence that the biological explanation is not true.

Dr. Kristensen claims.

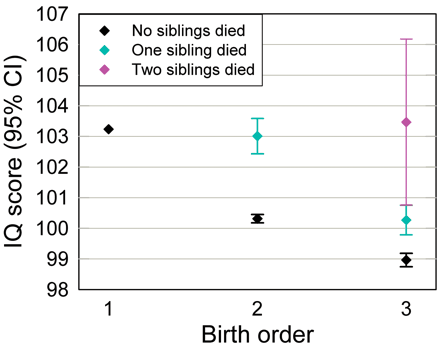Relation between birth order and IQ score. Mean IQ scores for male conscripts, first, second and third born to Norwegian mothers with single births only and first birth between 1967 and 1976, according to birth order and number of elder siblings who died in infancy (age < 1 year). Scores are adjusted for parental education level, maternal age at birth, sibling size, birth weight and year of conscription. Error bars show 95% confidence intervals. Source: Kristensen and Bjerkedal, Science, 22 June 2007.

This image shows that conscripts of first rank in social terms, no matter what their biological rank, scored the same as firstborn men. Men of birth order three who grew up as the second eldest child had IQ scores close to those of secondborns with no elder sibling loss.

Adjusted effects of birth order and social order on mean IQ scores with corresponding 95% confidence limits were obtained in multiple linear reg Linear regression showed that these associations were stronger in adjusted models and that the effect of birth order no longer was significant (P = 0.76) after accounting for social order (table S1).

Frank J. Sulloway at the University of California, Berkeley, who was not involved in the study but wrote an editorial accompanying it, said

There was some room for doubt about this effect before, but that room has now been eliminated.

In contrast, Joseph Lee Rodgers, a psychologist at the University of Oklahoma, was skeptical

Past research included hundreds of reported birth order effects that were not legitimate I’m not sure whether the patterns in the Science article are real or not; more description of methodology is required.

Questions

• How accurate do you think IQ scoring is? Would you expect IQ scores to vary over a person's lifetime? Does it depend on which test(s) you take? Might results be biased by cultural issues? How might you expect the IQ figures quoted in this study to be adjusted for such sources of variation?
• Why do you think the study ignored women? Might we expect identical results for women, a priori?
• Does it matter that the data is based only on 18 and 19 year olds, excluding all other age groups? What is the justification for extrapolating to other age groups?
• The Nobel prize winners example is surely not reliable given the small sample size. Discuss.
• Are you persuaded that three points on an I.Q. test may be material, either for the average across a large group or for an individual if cumulated over time?
• If someones IQ score can improve following the death of an older sibling, does this invalidate the merits of IQ tests as a standardised test of intelligence?
• How do you think the authors deal with cases involving remarriage or adoption?
• What do you think Rodgers meant by more description of (the) methodology is required?

Further reading

• The on-line Science article is a short and easy read: Explaining the Relation Between Birth Order and Intelligence, Petter Kristensen1 and Tor Bjerkedal, 316, 1717 (2007).
  • Did you know:
    • The relation between birth order and intelligence dates back to the polymath Sir Francis Galton's book English Men of Science: Their Nature and Nurture, published in 1874.
    • This book tablulates the results of his survey of features like the birth order, occupation and race of the parents of 190 members of the Royal Society.
    • Galton found more firstborn sons in prominent positions than what he attributed to chance.
    • Galton was the first to use the phrase nature verses nurture in this context.
  • Supplemental material is available on-line.
    • This includes computer printouts of the data format and the linear regression model results, from the Stata package, which were used to fit the data. Do they help your understanding of the methodology used?
• Sulloway wrote the 1996 book Born to Rebel: Birth Order, Family Dynamics, and Creative Lives.
  • This book was reviewed in Chance News 5.13.
• There is a discussion about this issue on the Statistical modeling, causal inference and social science blog, with additional links.

The game of Two up

Owen Dearricott is from Australia and when he taught the Dartmouth probability course he could not resist telling the students about Australia's famous coin tossing game Two-up and giving the students the problems related to the game:

In the game of Two up two coins are placed on a block of wood called a kip by the adjudicator and the player or spinner tosses or spins the coins by throwing them at least 3 feet above his head and letting them drop to the ground. The objective is for the spinner to get three double heads when he is in the ring. If in a spin he spins two heads he has headed them in which case he gets to spin again, if he spins a head and a tail he has oned them in which case it does not count as a success but he gets to spin again, if he spins two tails though he has tailed them and lost and passes the kip on to the next player. If he manages to head them three times he has won.

Owen ask his student's to find the probability of winning at Two up and the expected number of spins in a winning game of Two up?

Twoup was played by Australia's soldiers during World War I.

http://www.dartmouth.edu/~chance/forwiki/2p.jpg

After World War I it played on ANZAC Day, Australia's day to honor their solders. This was the only day it could be played legally. However, in Wickipedia we read:

As time passed, increasingly elaborate illegal "two-up schools" grew around Australia to the consternation of authorities but with the backing of corrupt police. The legendary Thommo's Two-up School, which operated at various locations in Sydney from the early years of the 20th century until well after World War II, was one of Australia's first major illegal gambling operations.

Legal Two-up arrived with its introduction as a "table" game at the new casino in Hobart in 1973 and it is still offered in some Australian casinos. "Two-up schools" in the Outback have also been legalised. The Wizard of Odds discribes here how Two up is played in casinos today.