Chance News 91
January 15, 2013 to February 28, 2013
Quotations
"As I wrote a couple years ago, the problem, I think, is that they (like many economists) think of statistical methods not as a tool for learning but as a tool for rigor. So they gravitate toward math-heavy methods based on testing, asymptotics, and abstract theories, rather than toward complex modeling. The result is a disconnect between statistical methods and applied goals.
"For the psychologists you’re looking at, the problem is somewhat different: they do want to use statistics to learn, they’re just willing to learn things that aren’t true."
Submitted by Paul Alper
"Hendry’s standing at the back window with a shotgun, scanning for priors coming over the hill, while a million assumptions just walk right into his house through the front door."
Submitted by Paul Alper
“If you want to eat sausage and survive, you should know what goes on in the factory. That dictum … most definitely applies to the statistical sausage factory where medical data is ground into advice.”
in “A Crash Course in Playing the Numbers”, The New York Times, January 28, 2013
Submitted by Margaret Cibes at suggestion of James Greenwood
"I’ve heard tell though, that Frequentists believe the Bayesian/Decision Theoretic stuff is metaphysical non-sense and were pushing the US government into bribing China to invade Taiwan 1000 times so that they could calibrate their Frequentist models. I haven’t heard anything about that proposal in a while so maybe it’s been dropped."
Submitted by Paul Alper
“Half of all advertising is wasted. I just don’t know which half. …. The same thing is true of Chinese statistics. Half of them are wrong. The problem is that we don’t know which half.”
This remark was made by an American lawyer who is collecting data from locally hired Chinese pollsters in order to provide potential investors with a more accurate picture of the Chinese economy.
Submitted by Margaret Cibes
Forsooth
"Greek Chief of Statistics Is Charged With Felony"
Think about what happened to the Italian scientist who failed to predict the earthquake... In the article we read
Greek prosecutors have charged the head of the country's statistics agency and two other board members with allegedly inflating Greece's 2009 deficit, that led to the country's first rescue loan from the European Union and the International Monetary Fund in May 2010, a judicial official said Tuesday.
"The president of the statistical agency, Andreas Georgiou and other two members are charged with felony violations for dereliction of duty and making false statements that damaged the Greek state," the official said...Mr. Georgiou denied wrongdoing and said that Greece's statistics standards where simply brought in line with the demands of Eurostat, the European statistical agency.
Submitted by Paul Alper
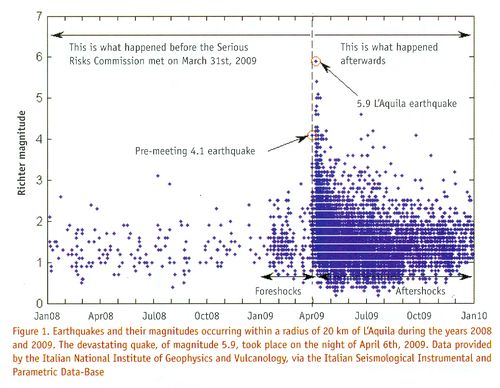
Aquila earthquake chart
“The L’Aquila earthquake: Science or risk on trial”
by Jordi Prats, Significance magazine, December 2012
Prats discusses the April 2009 Italian earthquake during which about 300 residents lost their lives. Readers will recall news about the 13-month trial of the six scientists (and a government official), who were each sentenced to six years in prison for “providing ‘inaccurate, incomplete and contradictory information’ on the probability and risk of an earthquake and for falsely reassuring the population.” (See “The perils of failed predictions”, Chance News 89, October-November 2012.)
Prats reports that, according to the Italian Macroseismic Database, "L’Aquila has suffered earthquakes of magnitude 6 or higher on 13 occasions in the period 1315-2005, approximately every 50 years." Also, he reports that, according to a 1988 seismology paper, “Alarm systems based on a pair of short-term earthquake precursors”, "[T]he probability of a weak shock or swarm being followed by a major shock in the following 2-5 days is very low, of the order of 1-5%."
Prats believes that the most important information for the public would have been the risk (in the sense of expected loss) of an earthquake, and not the just its likelihood, because such a risk assessment would have included both the probability of an earthquake and the expected loss in the event of an earthquake.
In any case, Significance Editor Julian Chamkin has given permission to post the following chart from the article (email of January 14, 2013):
Discussion
1. Based on the chart, would you have recommended that the Aquila public be informed, in March or April of 2009, that they should be prepared for a serious earthquake? (Note that, according to Wikipedia[1], someone who made a March 2009 prediction of a major earthquake was accused of being "alarmist," and “forced to remove his findings from the Internet.”)
2. Consider the Challenger spacecraft disaster in 1986. The O-ring chart made famous by Edward Tufte[2] suggested potential problems with launching a spacecraft at the near-freezing temperature at which it was actually launched. An online article, “Representation and Misrepresentation: Tufte and the Morton Thiokol Engineers on the Challenger”, discusses the role of the engineers in that decision, with respect to the information available to them and to their professional ethical responsibilities. Interested readers may also check out a Berkeley professor's Q&A activity sheet, “Challenger O-Ring Data Analysis”, about the Challenger O-ring issue.
3. While we're on the topic of decision-making based, at least partially, on charts, see the chart below, which shows U.S. presidential election results in Florida for a major-party (Gore) and minor-party (Buchanan) candidate. Based on the chart, what might you have recommended to an election official? See "Why Usability Testing Matters".
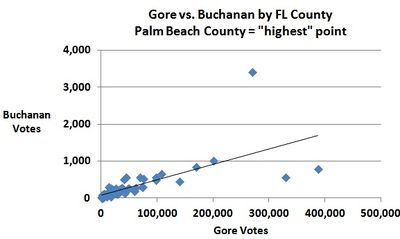
Submitted by Margaret Cibes
Re #3, Bill Peterson called attention to the article, "Voting Irregularities in Palm Beach, Florida", Chance magazine, 2001, which contains a similar chart comparing Buchanan's votes in the 1996 primary to those in the 2000 election. Remarkably, in 2012 we saw Palm Beach County back in election spotlight (Politico.com). This article quoted Palm Beach County GOP Chairman Sid Dinerstein as saying he wasn’t worried that the county would skew yet another presidential race: “We’re talking about 25,000 ballots in a state that is going to cast 8 million." Earlier in that article is a reminder that George W. Bush's 2000 final margin in Florida was 527 votes!
A(nother) Random Walk Down Wall Street
“Investments: Orlando is the cat's whiskers of stock picking”
by Mark King, The Observer, January 12, 2013
During the forty years between the first publication of Burton Malkiel's A Random Walk Down Wall Street (in 1973) through its most recent (10th) edition (in 2011) there have been numerous attempts to test Malkiel's contention that "a blindfolded chimpanzee throwing darts at the stock listings can select a portfolio that performs as well as those managed by the experts." (Not surprisingly, Chance News has also been following many of these efforts-- see below.)
The set-up here is typical: a panel of financial experts is pitted against a "random" process to choose, buy, and sell stocks, which in the current version is achieved through the antics of a cat named Orlando. "While the professionals used their decades of investment knowledge and traditional stock-picking methods", the article says, "the cat selected stocks by throwing his favourite toy mouse on a grid of numbers allocated to different companies." For an additional comparison, a third process of investing was included-- by a group of high school students. The Observer designed and oversaw the "portfolio challenge", as they called it, which was a year-long effort ending on December 31, 2012:
Each team invested a notional £5,000 in five companies from the FTSE All-Share index at the start of the year. After every three months, they could exchange any stocks, replacing them with others from the index. By the end of September the professionals had generated £497 of profit compared with £292 managed by Orlando. But an unexpected turnaround in the final quarter has resulted in the cat's portfolio increasing by an average of 4.2% to end the year at £5,542.60, compared with the professionals' £5,176.60.
The students fared the worst, ending down £160 for the year.
The chart below shows the 3-year activity of the FTSE All-Share index (from Bloomberg Market Data):
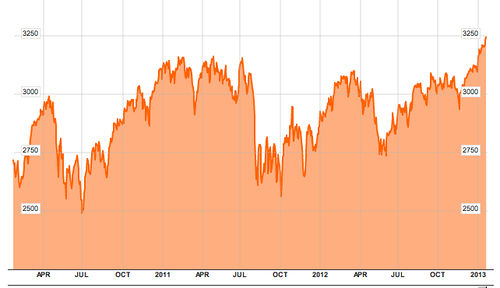
The starting and ending values for last year (12/30/11 to 12/31/12) are 2857.88 and 3093.41, yielding an 8.24% increase for the index. During the same period, Orlando's method produced a 10.84% increase, while the experts gained 3.52%.
Discussion
1. The details of Orlando's protocol are not provided in the article. Does it appear to be a random process? Why or why not? If not, can you devise a random process for Orlando to use?
2. The high school students who took part in the project attend the John Warner School (in Hertfordshire, England.) The school's deputy headteacher, Nigel Cook, is quoted: "The mistakes we made earlier in the year were based on selecting companies in risky areas. But while our final position was disappointing, we are happy with our progress in terms of the ground we gained at the end and how our stock-picking skills have improved."
Do you think the phrase our stock-picking skills have improved is warranted? Why or why not?
Submitted by Jeanne Albert
And another way to predict stocks!
Super Bowl indicator 'has promise'
by Steve Jordon, Ohama.com, 3 February 2013
As the article notes, the Super Bowl indicator was introduced by the sportswriter Leonard Koppett. His 1978 piece "Carrying Statistics to Extremes" appeared in the Sporting News. Up to that time, 11 Super Bowls had been played. Koppett wrote, "in all 11 years, whenever an old NFL team won the Super Bowl in January, the stock market rose during the next 11 months...and whenever an old AFL team won, the market finished that year lower." He clearly considered this a statistical fluke. Later in his article we find in bold type: "What does it all mean? Nothing!" You can the full article and more discussion the Chance News archives here. That edition featured the following quotation from Koppett:
Two tendencies (among others) seem fairly universal among 20th Century humans: a desire to make money as painlessly as possible and excessive willingness to believe that statistics convey valuable information.
Nevertheless, the legend of the Super Bowl indicator lives on. For the present article, Omaha.com sought out Bob Johnson, a Creighton University professor of finance, for this year's update on the trend. We read that in 35 out of the 46 Super Bowls up to this year, the indicator has correctly predicted the direction of the Dow Jones average, which is a success rate of 76%. The article continues
What's the explanation?
The stock market usually goes up anyway (33 of the last 46 years), and old NFL teams generally win the Super Bowl (33 of 46 years), so the two are likely to coincide more than average — 28 times, to be exact. Since 1966, former NFL teams have won 71.1 percent of the Super Bowls, and the Dow average has grown 71.7 percent of the time. By simple chance, the “predictor” should be correct 59.5 percent of the time. (We'll take the professor's word on the calculations.)
But statistically speaking, Johnson says, the 76 percent success rate is “very surprising” because the probability of the indicator being right 35 or more times out of 46 Super Bowls is only 1.41 percent.
The article appeared before this year's game, in which the Baltimore Ravens defeated the San Francisco 49ers. San Francisco is an old NFL team. But the Ravens migrated from Cleveland, where they were the Browns, another original NFL team. So as we are told here, the Ravens win is also good news for the market.
Discussion
1. An exercise for an intro statistics class might be to reproduce the 59.5% and 1.41% figures quoted above. Is this a "statisically significant" result?
2. Echoing Koppett, Johnson is quoted as calling the finding a "spurious correlation." On the other hand, the headline of the article says the indicator "has promise." So what is the message here?
Submitted by Bill Peterson
Fecal matter matters
When pills fail, this, er, option provides a cure
by Denise Grady, New York Times, 17 January 2013
In case you never worried about Clostridium difficile bacteria, the article points out that the disease caused by C. difficile bacteria “kills 14,000 people a year in the United States.” We read that “this stubborn and debilitating infection.. is usually caused by antibiotics, which can predispose people to C. difficile by killing normal gut bacteria. If patients are then exposed to C. difficile, which is common in many hospitals, it can take hold.”
The usual treatment involves more antibiotics, but about 20 percent of patients relapse, and many of them suffer repeated attacks, with severe diarrhea, vomiting and fever.
Hence, the use of fecal transplants from a healthy person into the gut of the one who is ill in order to reestablish a healthy gut:
Researchers say that, worldwide, about 500 people with the infection have had fecal transplantation. It involves diluting stool with a liquid, like salt water, and then pumping it into the intestinal tract via an enema, a colonoscope or a tube run through the nose into the stomach or small intestine.
Although reported success rates of fecal transplants have been high, evidenced based medicine requires a randomized controlled trial. This can be found at the January 17, 2013 issue of the New England Journal of Medicine.
We randomly assigned patients to receive one of three therapies: an initial vancomycin regimen (500 mg orally four times per day for 4 days), followed by bowel lavage and subsequent infusion of a solution of donor feces through a nasoduodenal tube; a standard vancomycin regimen (500 mg orally four times per day for 14 days); or a standard vancomycin regimen with bowel lavage. The primary end point was the resolution of diarrhea associated with C. difficile infection without relapse after 10 weeks.
The study was stopped after an interim analysis. Of 16 patients in the infusion group, 13 (81%) had resolution of C. difficile–associated diarrhea after the first infusion. The 3 remaining patients received a second infusion with feces from a different donor, with resolution in 2 patients. Resolution of C. difficile infection occurred in 4 of 13 patients (31%) receiving vancomycin alone and in 3 of 13 patients (23%) receiving vancomycin with bowel lavage (P<0.001 for both comparisons with the infusion group). No significant differences in adverse events among the three study groups were observed except for mild diarrhea and abdominal cramping in the infusion group on the infusion day. After donor-feces infusion, patients showed increased fecal bacterial diversity, similar to that in healthy donors, with an increase in Bacteroidetes species and clostridium clusters IV and XIVa and a decrease in Proteobacteria species.
Discussion
1. The infusion group had 13 successes out of 16. The combined non-infusion group had 7 successes out of 26. Use whatever statistics package you fancy and carry out a t-test and CI for two proportions to show that the treatment is statistically significant.
2. Clearly, the medical world, at least as seen through the eyes of journalists, implicitly believes that this infusion treatment is clinically (i.e., practically) significant. However, after reading the two articles mentioned and any of the many others about the New England Journal of Medicine study found via Google, what ingredients are missing when it comes to clinical significance?
3. This randomized clinical trial is referred to as an open-label clinical trial. What does that mean and why was that necessary?
4. According to the original journal article, “The study was stopped after an interim analysis.” What conditions (good and bad) would lead to a randomized clinical trial being stopped?
5. No discussion of the usefulness of transplanting fecal material would be complete without mentioning "Coprophagia" and koala bears. Go to here to see how common coprophagia is among diverse species.
Submitted by Paul Alper
Follow-up
Paul wrote to point out that references to C.difficile bacteria and then fecal transplant appear on page 5 of The boy with a thorn in his joints (New York Times, 1 February 2013). He adds, "One begins to wonder how frequently antibiotics lead to gut trouble and what the article refers to as 'gut leakage.' However, to my mind the article leans too heavily towards the benefits of alternative medicine."
Shower risks
That daily shower can be a killer
by Jared Diamond, New York Times, 28 January 2013
Jared Diamond won the 1998 Pulitzer Prize for his book Guns, Germs and Steel. His most recent bool is The World Until Yesterday: What Can We Learn From Traditional Societies. In this article he describes "the biggest single lesson that I’ve learned from 50 years of field work on the island of New Guinea: the importance of being attentive to hazards that carry a low risk each time but are encountered frequently."
He relates an experience where the islanders refused to make camp near a large dead tree that had stood in that state for years, out of concern that this might be the day it falls. For a parallel in our modern lives, he cites the risk of falling in the shower. He reckons that most people would by happy to ignore this if they thought the chance was only 1-in1000. But he then calculates
Life expectancy for a healthy American man of my age is about 90. (That’s not to be confused with American male life expectancy at birth, only about 78.) If I’m to achieve my statistical quota of 15 more years of life, that means about 15 times 365, or 5,475, more showers. But if I were so careless that my risk of slipping in the shower each time were as high as 1 in 1,000, I’d die or become crippled about five times before reaching my life expectancy. I have to reduce my risk of shower accidents to much, much less than 1 in 5,475.
The National Safety Council website maintains a page entitled The Odds of Dying From..., where you can find the annual risk of death from various causes. As duly noted there: "The odds of dying are statistical averages over the whole U.S. population. They do not necessarily reflect the chances of death for a particular person from a particular external cause. Any individual's odds of dying from various external causes are affected by the activities in which they participate, where they live and drive, what kind of work they do, and other factors." That caveat is well-illustrated by the following cartoon, (from XKCD).

Discussion
1.What assumptions are implicit in the shower calculation above?
2. Of course, you are not going to die five times! But, under these assumptions, what is the chance of at least one accident in 5475 showers?
Submitted by Bill Peterson
More on Nate Silver's new book
See this discussion in Chance News 90 of Nate Silver's The Signal and the Noise.
Following up on this post, Paul Alper sent links to two more reviews from Andrew Gelman's blog. Paul also noted the spirited Bayesian vs. frequentist exchange in the comments there. In that vein, he sent the following cartoon
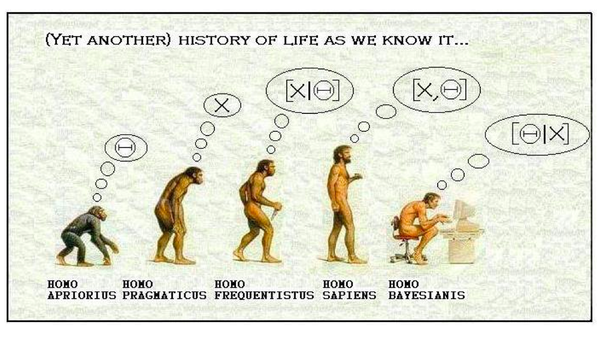
which has appeared in various places on the web (see here and here).
Historic atlases available for chart junkies
“The Motley Roots of Data Visualization in 19th Century Census Charts”
by Jeffrey Rotter, the Atlantic CITIES, January 28, 2013
While looking for ways to visualize old U.S. census data, Jonathan Soma, a self-styled stats junkie, “discovered a trove of maps and charts in a musty backroom of the Library of Congress web site.” These were three Statistical Atlases of the U.S.A. (1870, 1880, 1890).
Soma has compiled the three atlases (384 pages), into A Handsome Atlas and organized the pages into eight topics and eight visualizations. The reviewer writes:
And they are wonders to behold, with or without the numbers.
(For other, albeit non-atlas, charts, see “Choices in statistical graphics: My stories”, for Andrew Gelman's slides from a talk he gave at the New York Data Visualization Meetup on January 14, 2013.)
Submitted by Margaret Cibes
Stargate and Bayes
Statisticians often weigh in on matters psychic either to present or to debunk the phenomenon. For example, see this look at Bem’s ESP study and this additional commentary. Fortunately, most research on psychic phenomena while often generating much ink and chatter, is neither dangerous nor costly. An exception would be the Stargate Project.
The Stargate Project was the umbrella code name for several sub-projects established by the U.S. Federal Government to investigate claims of psychic phenomena with potential military and domestic applications, particularly "remote viewing” ability to psychically "see" events, sites, or information from a great distance.
These projects were active from the 1970s through 1995, and followed up early psychic research done at The Stanford Research Institute, (SRI), Science Applications International Corporation (SAIC), The American Society for Psychical Research, and other psychical research labs.
The head of the research was Major General Albert Stubblebine, who
was convinced of the reality of a wide variety of psychic phenomena. He required that all of his Battalion Commanders learn how to bend spoons a la Uri Geller, and he himself attempted several psychic feats, even attempting to walk through walls.
Eventually, during those scary cold-war decades
[T]he CIA terminated the 20 million dollar project, citing a lack of documented evidence that the program had any value to the intelligence community. Time magazine stated in 1995 [that] three full-time psychics were still working on a $500,000-a-year budget out of Fort Meade, Maryland, which would soon close.
Before the termination,
a retrospective evaluation of the results was done. The CIA contracted the American Institutes for Research for an evaluation. An analysis conducted by Professor Jessica Utts showed a statistically significant effect, with gifted subjects scoring 5%-15% above chance, though subject reports included a large amount of irrelevant information, and when reports did seem on target they were vague and general in nature. Ray Hyman argued that Utts' conclusion that ESP had been proven to exist, especially precognition, "is premature and that present findings have yet to be independently replicated."
Here is a 58-minute video, “The strength of evidence versus the power of belief: Are we all Bayesians?”, in which Utts describes in detail how the psychic research was done and what can be learned from the study. She eventually does a frequentist analysis of the remote viewing which had 56 studies in which the supposed probability of success due to chance on any one trial is .25. When by chance alone, if .25 is assumed for the null, 709 “hits” out of 2124 trials thus yields a proportion of .334, leading to a p-value of 2.26 x 10**-18 and a confidence interval of .314 to .354.
She then does a Bayesian analysis using possible prior beliefs of a skeptic (true proportion is tightly around .25), a believer (most likely value is around .33) and an open-minded person (most likely value is around .25 but can go near the .33) in order to illustrate how prior beliefs influence the posterior result. She then concludes with the assertion that remote viewing would be a good classroom activity for illustrating Bayesianism.
Discussion
1. Use any available stats package to show 709 hits out of 2124 trials does yield the results listed above except for the 2.26 x 10-18. Why did your stats package not print out that last number but instead merely reported “p-value = 0”?
2. Somewhere around the 45th minute, she mentions the difficulty posed by the “stacking effect.” What is it and why is it a problem when testing several participants?
3. National Geographic pictures play an important part in the video. At about the 17th minute mark she shows a drawing made by one of the psychics that closely matches the unknown picture. Why is this less than surprising?
4. At about the 10th minute she distinguishes four kinds of psychic phenomena: telepathy, clairvoyance, precognition and correlation. Pick a phenomenon and design an experiment to show whether it exists. If you are a Bayesian and using a conjugate prior given by the Beta distribution (around the 33rd minute), what are your values for the parameters a and b?
5. If evidence for psychic phenomena does not exist, why are there so many believers?
6. Applying statistical procedures to unearth/ verify something which doesn’t exist is not confined to psychic phenomena. In this Chance News post Dr. Leonard Leibovici, an Israeli medical doctor, comments on his satirical BMJ paper in which 4-10 years after the fact, retroactive intercessory prayer had a statistically significant result regarding patient survival in a (double-blinded) randomized clinical trial:
The purpose of the BMJ [British Medical Journal] piece was to ask the reader the following question: Given a 'study' that looks methodologically correct, but tests something that is completely out of our frame (or model) of the physical world (e.g., retroactive intervention or badly distilled water for asthma) would you believe in it?
To deny from the beginning that empirical methods can be applied to questions that are completely outside our scientific model of the physical world. Or in a more formal way, if the pre-trial probability is infinitesimally low, the results of the trial will not really change it, and the trial should not be performed. This is what, to my mind, turns the BMJ piece into a 'non-study' although the details provided in the publication (randomization done only once, statement of a wish, analysis, etc.) are correct.
Compare and contrast Leibovici’s retroactive intercessory prayer study with the Stargate Project to determine the similarities and the differences.
Submitted by Paul Alper
Should you help your kids pay for college?
Parents’ financial support may not help college grades
by Tamar Lewin, New York Times, 15 January 2013
We read in the opening paragraph:
Parents saving for college costs, take heed: A new national study has found that the more college money parents provide — whether in absolute terms or as a share of total costs — the lower their children’s college grades.
Along with the headline, this invites readers to leap to causal conclusions. Maybe students who pay their own way are more motivated and study harder. A "dose-response" effect is even suggested: the more money parents put up, the worse students performed.
The study, entitled "More Is More or More Is Less? Parental Financial Investments During College," was authored by Laura T. Hamilton of the University of California-Merced, and appeared in the American Sociological Review. An abstract is available here, where we read "Rather than strategically using resources in accordance with parental goals, or maximizing on their ability to avoid academic work, students are satisficing...[S]tudents with parental funding often perform well enough to stay in school but dial down their academic efforts."
On his blogpost That claim that students whose parents pay for more of college get worse grades (22 January 2013), Andrew Gelman was skeptical. He writes: "The problem I’m worrying about is selection, what is sometimes called 'survivorship bias.' If you’re not doing so well in college but it’s being paid for, you might stay. But if you’re paying for it yourself, you might just quit."
Submitted by Bill Peterson
Online polling pretty successful
“A More Perfect Poll”, by Molly Ball, The Atlantic, March 2013
The article describes the difficulty pollsters have in reaching people by telephone, whether cellphone or landline users, and the relatively more success pollsters had in using online polls to predict election results in 2012.
The author cites Nate Silver:
When [he] compared polls in the final weeks of the presidential campaign with the outcome, Internet polls had an average error of 2.1 points, while telephone polls by live interviewers had an average error of 3.5 points.
Traditionalists are concerned that online polls may not achieve a “probabilistic” sample because “[j]ust about everyone who votes has a phone, but only 80 percent of American adults have Internet access, and those who don’t are predominantly older and lower-income.”
And the author reports,
“The New York Times - ”the very paper that hosts FiveThirtyEight, Silver’s blog—still refuses to cite Internet-based polls in its news reporting. Maybe it’s time for The Times to get with the times.”
Discussion
1. Given similar distributions of sample responses from two polls, how would you explain a difference in the margin of error of a common 95% confidence interval? How might that support an argument in favor of online polling?
2. Do you think that there is a relationship between one’s likelihood of voting and one’s likelihood of having Internet access, despite age or economic status? Do you think that such a relationship might tend to make online polling more reliable?
3. Do you think that The New York Times should re-consider its policy?
Submitted by Margaret Cibes
Population implosion?
“America's Baby Bust”, The Wall Street Journal, February 20, 2013
This article is a review of a new book, What to Expect When No One’s Expecting: America’s Coming Demographic Disaster. The author discusses the falling fertility rate in the U.S. and elsewhere and how it may negatively affect economies in serious ways. The author states that “97% of the world’s population now lives in countries where the fertility rate is falling.”
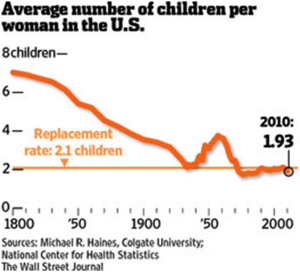
Chance readers might like to read/re-read the following two books that provided dire warnings in the opposite direction, that of overpopulation:
(1) An Essay on the Principle of Population, by Thomas Malthus, 1798;
(2) The Population Bomb, by Paul and Anne Ehrlich, 1968.
Submitted by Margaret Cibes