Chance News 100
June 6, 2014 to August 13, 2014
Quotations
"Steve Ziliak, a critic of RCTs [randomised controlled trials], complains about one conducted in China in which some visually-impaired children were given glasses while others received nothing. The case against the trial is that we no more need a randomised trial of spectacles than we need a randomised trial of the parachute."
Submitted by Paul Alper
“My experience is that even the most mathematically competent often find probability a subject that is difficult to use and understand. The difficulty stems from the fact that most problems in probability cannot be solved by using cookbook recipes as is the case in calculus, but each problem again requires creative thinking.”
(see more on Tijms' devil's penny puzzle below)
Submitted by Bill Peterson
“If the statistics courses are not providing basic statistical intuition, it is not necessarily because they failed to cover the material, but perhaps just the opposite. That is, by covering so many topics, they may yield a poor signal to noise ratio when it comes to the basics.” [p. 269, author’s emphasis]
“I refer to … ‘consumer stochastics’ …. This differs from the overall field of statistics only in its target audience. Whereas statistics has aided scientists … in almost every discipline …, consumer stochastics is aimed at non-scientists …, who face uncertainty on a regular basis, that is, most professionals.” [p. 270]
Statistics and Public Policy, 1997
Submitted by Margaret Cibes
"The point is that just because one event sometimes follows another it does not follow that the following event is caused by that by which it is preceded. That this fallacy does, in fact, regularly get past your average journalist entitles it to a name: the post hoc, passed back fallacy."
"If only they could invent a drug that would cure journalistic impotence and permit hacks to have some meaningful intercourse with science. Now there would be a medical breakthrough."
Cambridge University Press, 2003, p. 109
Submitted by Margaret Cibes
Forsooth
One sentence too many?
“At issue was how highly correlated the prices of various subprime mortgage bonds inside a CDO might be. Possible answers ranged from 0 percent (their prices had nothing to do with each other) to 100 percent (their prices moved in lockstep with each other). Moody’s and Standard & Poor’s judged the pools of triple-B-rated bonds to have a correlation of around 30 percent, which did not mean anything like what it sounds. It does not mean, for example, that if one goes bad, there is a 30 percent chance that the others will go bad too. It means that if one bond goes bad, the others experience very little decline at all.”
Submitted by Margaret Cibes
“When confronted with data from the Centers for Disease Control that seemed to provide scientific refutation of her claims [that vaccines caused autism, Jenny] McCarthy responded, ‘My science is named Evan [her son] and he’s at home. That’s my science.’ …. She is fond of saying that she acquired her knowledge of vaccinations and their risks at ‘the University of Google.’” [p. 79]
“[Dr. Andrew] Weil doesn’t buy into the idea that clinical evidence is more valuable than intuition. Like most practitioners of alternative medicine, he regards the scientific preoccupation with controlled studies, verifiable proof, and comparative analysis as petty and one dimensional.” [p. 257]
"[T]he National Center for Complementary and Alternative Medicine is the brainchild of Iowa senator Tom Harkin, who was inspired by his conviction that taking bee pollen cured his allergies …. There is no evidence that bee pollen cures allergies or lessens their symptoms. ….
In Senate testimony in March 2009, Harkin said he was disappointed in the work of the center because it had disproved too many alternative therapies. ‘One of the purposes of this center was to investigate and validate alternative approaches. Quite frankly, I must say publicly that it has fallen short,’ Harken said.” [pp. 174, 180]
“I don’t have either APOE4 allele, which is a great relief. ‘You dodged a bullet,’ my extremely wise physician said when I told him the news. ‘But don’t forget they might be coming out of a machine gun.” [p. 220]
Submitted by Margaret Cibes
"Another example of that interest was data from TiVo showing that although four of the top five streamed games of the tournament in homes with TiVo DVRs involved the United States team, six of the 10 most-streamed games involved teams from other countries." [One must bear in mind that the US played in exactly four games in the World Cup!]
Submitted by David Czerwinski
The Guardian reported that the British intelligence agency GCHQ secretly collected images of Yahoo webcam chats in bulk. The program was called Optic Nerve, according to documents revealed by Edward Snowden, and many of the images contain sexually explicit ("undesirable") material. The Guardian article discusses Yahoo's response to this report, the legality of the Optic Nerve and other GCHQ efforts, how GCHQ handled explicit images, and how the agency attempted to estimate the proportion of Yahoo accounts with explicit images. The article contains this paragraph from one of the GCHQ documents:
- "A survey was conducted, taking a single image from each of 323 user ids. 23 (7.1%) of those images contained undesirable nudity. From this we can infer that the true proportion of undesirable images in Yahoo webcam is 7.1% ± 3.7% with confidence 95%."
However, the calculation seems to have been made at the 99% confidence level. For 95% confidence, the margin of error would be smaller, only ±2.8%.
Submitted by Alan Shuchat
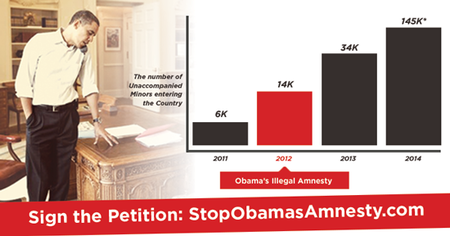
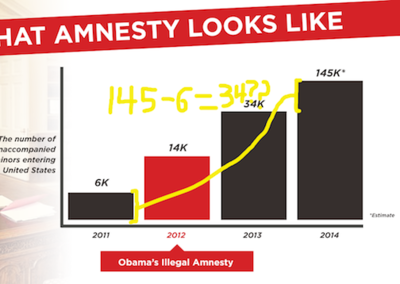
Yglesias adds: "It's not clear exactly why Cruz's team made the chart this way. Perhaps they thought that showing a huge surge happening with a one-year delay would make the argument less convincing. Perhaps they just don't know how to make charts."
Submitted by Priscilla Bremser
The Oxford comma: A pressing issue?
Elitist, superfluous, Or popular? We polled Americans on the Oxford comma
By Walt Hickey, FiveThirtyEight, 17June 2014
A grammatical point of controversy: should you use a comma before the "and" in a list of more than two items? As reported in the article:
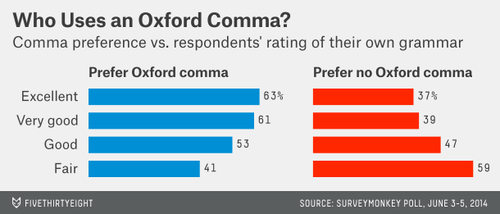
We asked respondents which sentence was, in their opinion, more grammatically correct: “It’s important for a person to be honest, kind and loyal.” Or: “It’s important for a person to be honest, kind, and loyal.” The latter has an Oxford comma, the former none.
Among 1129 Americans responding, the Oxford comma was preferred, 57% to 43%. Interestingly, those in favor tended to have a higher opinion of their own grammatical skills, as shown in the accompanying graph
Lest you get the impression that this is simply a matter of taste, see The best shots fired in the Oxford comma wars. Among the amusing examples there:
Pro: "She took a photograph of her parents, the president, and the vice president."
This example from the Chicago Manual of Style shows how the comma is necessary for clarity. Without it, she is taking a picture of two people, her mother and father, who are the president and vice president. With it, she is taking a picture of four people.
Con: "Those at the ceremony were the commodore, the fleet captain, the donor of the cup, Mr. Smith, and Mr. Jones."
This example from the 1934 style book of the New York Herald Tribune shows how a comma before "and" can result in a lack of clarity. With the comma, it reads as if Mr. Smith was the donor of the cup, which he was not.
Or this example, from the NYT "After Deadline" blog (the italicized passage appeared in a news story):
Already, people wear computers on their faces, robots scurry through factories and battlefields and driverless cars dot the highway that cuts through Silicon Valley.
Battlefields and driverless cars dot the highway? We may have decided to omit a comma after “battlefields” because of our usual avoidance of the so-called serial comma. But commas generally are used between independent clauses, and clarity certainly required one here.
Submitted by Paul Alper
Interpreting climate change probabilities
Bob Griffin sent a link to the following
- The interpretation of IPCC probabilistic statements around the world
- by David V. Budescu, et al, Nature Climate Change, 20 April 2014
which he describes as "an intriguing look at how folks in different cultures around the world interpret the verbal statements of uncertainty that the Intergovernmental Panel on Climate Change uses. They found that an alternative presentation format (verbal terms with numerical ranges) improves the correspondence between the IPCC guidelines and public interpretations. The alternative presentation format also produces more stable results across cultures."
On the Nature site, only the abstract is available to non subscribers, but you can read more about the study design in this Fordham University press release. As described there:
The study asked over 11,000 volunteers in 24 countries (and in 17 different languages) to provide their interpretations of a the intended meaning and possible range of 8 sentences form the IPCC report that included the various phrases. For example, one sentence read: “It is very likely that hot extremes, heat waves, and heavy precipitation events will continue to become more frequent.” Only a small minority of the participants interpreted the probability of that statement consistent with IPCC guidelines (over 90 percent), and the vast majority interpreted the term to convey a probability in around 70 percent.
A similar effect was observed with other phrases: When verbal descriptions were given without numerical ranges, readers tended to interpret the probabilities as being closer to 50 percent than intended by the guidelines.
The Wikipedia entry on Words of estimative probability provides some perspective on this, illustrating that different verbal descriptions are used in different fields. The phrase "words of estimative probability" (WEP) is described as originating in the intelligence community. (The lack of preparation prior to the 9/11 attacks is cited as a famous failure in risk communication.) But as described here, a different set of phrases are used in the medical community in the context of informed patient decision making.
Summer reading
Past, Present, and Future of Statistical Science, Chapman and Hall/CRC, 2014
This free pdf download is the result of a project of the Committee of Presidents of Statistical Societies (COPSS) to assemble from almost 50 statisticians their reminiscences, personal reflections, and perspectives on the discipline and profession, as well as advice for the next generation. The contributions are relatively short, very good reads.
Submitted by Margaret Cibes
Finding lost aircraft
How statisticians found Air France Flight 447 two years after it crashed into Atlantic
MIT Technology Review, 27 May 2014
In 2009, an Air France disappeared while crossing over the Atlantic Ocean. Conventional searched were unable to locate the wreckage, but the article describes subsequent use of Bayesian statistical techniques helped lead to its discovery. A key step in the analysis involved modeling the possibility that electronic beacons had failed during earlier searches; in fact, the plane was ultimately found in an area that had previously been searched.
Reading this story naturally makes one think of the recent disappearance of Malaysia Airlines Flight 370. Indeed, see:
- How statisticians could help find that missing plane, by Carl Bialik, FiveThirtyEight, 17 March 2014
Submitted by Jeanne Albert
Probability of precipitation
John Emerson sent a link to the following:
Pop quiz: 20 percent chance of rain. Do you need an umbrella?
“All Things Considered,” NPR, 22 July 2014
This is part of a weeklong series on NPR, called Risk and reason, that explores people's understanding of chance. Noting that weather forecasts represent an almost daily encounter with probability statements, NPR interviewers set out to explore what the person in the street understands by the phrase “20 percent chance of rain.” You can listen to some responses in the audio segment (about 7.5 minutes) provided at the above link, or read the synopsis there. Not surprisingly, there a variety of answers, most not very scientific.
NPR listeners pointed out the the segment itself failed to produce a succinct answer, so NPR produced a short followup story the next day Confusion with a chance of clarity: Your weather questions, answered (23 July 2014). Included there were descriptions from two meteorology experts. Eli Jacks, of the National Weather Service said:
There's a 20 percent chance that at least one-hundreth of an inch of rain — and we call that measurable amounts of rain — will fall at any specific point in a forecast area.
Jason Samenow, of the Capital Weather Gang at the Washington Post offered this:
It simply means for any locations for which the 20 percent chance of rain applies, measurable rain (more than a trace) would be expected to fall in two of every 10 weather situations like it.
More detailed discussion can be found at this FAQ page from NOAA, where we read
Mathematically, PoP [probability of precipitation] is defined as follows:
- PoP = C x A where "C" = the confidence that precipitation will occur somewhere in the forecast area, and where "A" = the percent of the area that will receive measureable precipitation, if it occurs at all.
Discussion
Are the two weather experts quoted above saying the same thing? Do their descriptions square with the mathematical definition?
The "Devil’s Penny" puzzle
Henk Tijms and the devil’s penny
by Gary Antonick, Numberplay blog, New York Times, 3 March 2014
The following puzzle was created by emeritus Professor Henk Tijms of Vrije University in Amsterdam.
Ten boxes are placed in front of you and money is put into each box: two dollars, for example, goes in one of the boxes; five dollars in another box, and so on. You’re able to see each of the values. An eleventh box containing a Devil’s penny is added to the mix. The boxes are then closed and rearranged so that you can’t tell which box contains which amount of money — or if a particular box contains the dreaded Devil’s penny. You may then open up, one by one, as many boxes as you’d like and keep the money inside — but if you open the box with the Devil’s penny you lose everything. When should you stop?
The article notes that the solution has an appealingly simple form: To maximize the expected value of your winnings, you should stop when your accumulated fortune is greater than or equal to the amount of money remaining in unopened boxes (of course, if you get the Devil’s penny you are forced to stop with nothing). Prof. Tijms notes that a formal proof of optimality would rely on the Bellman equation from dynamic programming; nevertheless, he was pleased to find that several readers’ comments revealed key insights. You may want to look through the full set of these, which include detailed responses from Prof. Tijms, at the link above.
Indeed, the article itself contains the seeds of a solution by backward induction. Consider the number of boxes remaining unopened. If there is only one, it must contain the devil’s penny, so you stop. If there are two, then one is the devil’s penny and one has money. Since you are equally likely to get either by continuing, it makes sense (in expected value terms) to stop unless there is more money remaining than you already have won.
One of the interesting features here is that the optimal strategy considers only the total money available, not how is distributed across the boxes. To describe this, we borrow notation from one of the commenters (“Matt”). Suppose that n boxes remain, you have won W dollars so far, and R dollars remain. Then the conditional expected value of a box, given that it is not the devil’s penny, is given by R/(n-1), regardless of now the R dollars are distributed (a consequence of the random rearrangement of the boxes). Your expected fortune by continuing is therefore: [W + R /(n-1)] * [(n-1)/n] + (0) *(1/n). The strategy is to continue if this exceeds W. Solving the inequality gives the simple condition R > W.
The article describes two more involved versions of the puzzle, with an interactive feature for each scenario so that you can develop a feel for the play. Also, a colleague of Prof. Tijms has provided a full online simulation for the first version.
Submitted by Bill Peterson
Online chatter among drug trial participants
“Researchers Fret as Social Media Lift Veil on Drug Trials”
by Amy Docker Marcus, The Wall Street Journal, July 29, 2014
Subtitled “Online Chatter Could Unravel Carefully Built Construct of 'Blind' Clinical Trials,” this article describes some of the potentially negative effects that the increasing social media discussions among participants could have on drug trials. For example, participants could:
(a) discover whether they were in a treatment or a placebo group;
(b) drop out if they suspect they are in a placebo group;
(c) report symptoms inaccurately, or not at all, in order to stay in the trial;
(d) discourage others from remaining in, or even joining, a trial if experiences were not positive.
According to one drug company exec, “The FDA is going to have to figure out how to accommodate social media.” A Pfizer researcher says that a patient “helped him realize that it's not the patients who will change, but the researchers who have to change. …. [U]ltimately patients are human beings. They are going to talk.”
Perhaps a bright note:
A Duke University researcher says that the information patients share online can turn out to be incorrect. Before revealing the drug information at the conclusion of a trial, he often asks patients to guess whether they got active drug. "Most times they don't get it right," he says.
Submitted by Margaret Cibes
Cautions on polls
How to read the polls in this year's midterms
by Nate Cohn, "The Upshot" blog, New York Times, 10 July 2014
In forecasts of the 2012 presidential election, models based on aggregates of polling results famously outperformed political pundits. Cohn wonders whether such models can be as successful in the current climate. He writes:
So far this year, 65 percent of polls in Senate battlegrounds have been sponsored or conducted by partisan organizations, and an additional 10 percent were conducted by Rasmussen, an ostensibly nonpartisan firm that leans conservative and has a poor record.
He follows up with a detailed discussion of the polling situation in five states where a sitting Democratic senator faces a strong challenge.
A different spin on polls was given in an op/ed piece following Eric Cantor's primary loss in the spring:
Why polling fails: Republicans couldn’t predict Eric Cantor’s loss
by Frank Luntz, New York Times, 11 June 2014
Luntz (whose firm Luntz Global does polling and communications work) has some curious comments on polls. He writes:
The simple truth remains that one in 20 polls — by the simple rules of math — misses the mark. That’s why there is that small but seemingly invisible “health warning” at the end of every poll, about the 95 percent confidence level. Even if every scientific approach is applied perfectly, 5 percent of all polls will end up outside the margin of error. They are electoral exercises in Russian roulette. Live by the poll; die by the poll.
His recommendation is more reliance on face-to-face interview rather than impersonal polling:
Ironically enough in this wired-up age, the face to face remains a fundamental component of exploring voter mind-set. It is only by being in a room with voters that you can truly get the answer you need. It is about asking the right questions of the right people, and demanding honest answers.
The result that inspired this piece was actually an internal poll by the Cantor campaign. In The Eric Cantor upset: What happened?, Harry Enten of FiveThirtyEight.com outlines the general problems with such polls, and the less-than-stellar record of Cantor's polling firm in particular. (See also these comments on internal polls from Chance News 90.)
Discussion
1. If people's responses to polls don't correspond to their actual voting behavior, what kind of error is this? Is it covered by the 5 percent "health warning"?
2. How do you think Luntz proposes to get the "right people" in his sample?
Submitted by Bill Peterson
Anchors, ultimatums and randomization
William Poundstone writes wonderful, interesting books, veritable page turners. Some of his previous works were reviewed in Chance News here and here. Because he has set such a personal high bar, his latest two books while fun to read, don’t quite match his earlier output.
His 2010 book, Priceless: The Myth of Fair Value (and How to Take Advantage of It) focuses on the concept of anchoring, which Wikipedia describes as
A person begins with a first approximation (anchor) and then makes incremental adjustments based on additional information. These adjustments are usually insufficient, giving the initial anchor a great deal of influence over future assessments.
Thus says Poundstone, anchoring is beloved by behavioral economists, market consultants, advertisers, marketers, psychologists, attorneys and any other entities that wish to influence/fleece the unwary consumer/opponent. In essence, the public and the individual are easily manipulated by the mere mention of a number--a high number elicits high numbers and a low number brings forth low numbers. For example on page 11, if a (meaningless) random number (from a rigged spinning wheel) is 65, the participants claimed (on average) that the percentage of African nations in the U.N. is 45 percent whereas if the (meaningless) random number (from a rigged spinning wheel) is 10, the participants claimed (on average) that the percentage of African nations in the U.N. is 25 percent.
In case you are wondering, the correct fraction of African U.N. member nations is 23 percent.
Much of the rest of the book is devoted to tales of how anchoring and its offshoots can be used to swindle the general public. He turns the famous Oscar Wilde saying “A cynic is a man who knows the price of everything, and the value of nothing” on its head in the sense that, just as with “value,” there is no such thing as price; for instance, price is easily manipulated by means of lowering the weight of a package while keeping the price the same as before. Another common commercial technique is to run non-special special discounts.
Less well-known is the procedure supermarkets employ:
Shoppers open their wallets wider when moving through a store in a counterclockwise direction. On average, these shoppers spend $2 more a trip than clockwise shoppers…[Because] North Americans see shopping carts as ‘cars” to be driven to the right…By this theory, the right-handed majority finds it easier to make impulse purchases when the wall or shelf is to the right…[resulting in] markets putting their main entrance on the right of the store’s layout to encourage counterclockwise shopping
Particularly amusing is his Chapter 27, “Menu Psych,” where he demonstrates how a restaurant menu can be designed to avoid “A diner who orders based on price” because said diner “is not a profitable diner.”
The real agenda of the $110 price [of the seafood plate] is probably to induce customers to spring for the $65 Le Grand plate just to the left of it or the more modest seafood orders below it.
This modus operandi of an absurdly overpriced option in order to induce the buyer to choose a slightly less overpriced option can be applied to many fields from handbags to stadium seats and imported wine.
Then there is the ultimatum game:
[T]he ultimatum game is a game often played in economic experiments in which two players interact to decide how to divide a sum of money that is given to them. The first player proposes how to divide the sum between the two players, and the second player can either accept or reject this proposal. If the second player rejects, neither player receives anything. If the second player accepts, the money is split according to the proposal. The game is played only once so that reciprocation is not an issue.
Obviously, the word “game” is a euphemism and particularly amusing is Poundstone’s discussion of Jack Welch’s divorce proceedings whereby Welch, the former head of GE, made an initial offer which his wife refused resulting in all the lawyers involved profiting mightily.
As negotiations dragged on, Jack was offering Jane a temporary allowance of $35,000 a month. To a woman of Jane’s sense of entitlement, that didn’t go far enough [!]. It was time for Jane to play the ultimatum game.
Eventually, he blinked and
By one calculation, Jane’s ultimatum had cost the couple $2.5 million a year for the rest of their lives.
Poundstone’s 2014 book, Rock Breaks Scissors: A Practical Guide to Outguessing & Outwitting Almost Everybody spotlights the role randomness can play in competitive games such as the classic “rock, scissors, paper,” but also salary negotiations, computer passwords, multiple-choice tests, financial fraud, office pools, stock market investing, the Oscar pools. The chapters tend to be short with a recap at the end of each chapter.
Rock, scissors, paper is a well known betting game which exemplifies non-transitivity: A > B, B > C but C > A where the symbol “>” means dominates.
His Chapter 13, “How to Outguess Ponzi Schemes” concludes with
Be suspicious when too many numbers just top a psychologically significant threshold.
Although he doesn’t say so, this is reminiscent of p-hacking whereby frequentists’ p-values just go under the magical .05 in order to convince journal reviewers that the study should be published.
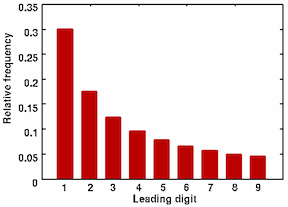
The most interesting chapter for statisticians is Chapter 11, “How to Outguess Fake Numbers.” He looks at the famous Benford Law of the leading digit which, to the surprise of many a convicted fraudster, is not a uniform distribution where the digits are equally likely, each appearing with probability 1/9. From Plus magazine we have the following plot of the distribution of the leading digit:
In this age of password hacking, Poundstone proposes using randomization and mnemonics to foil the hackers. For example, for the random password RPM8t4ka
RPM8t4ka might become revolutions per minute, 8 track for Kathy.
Big Data is the rage these days, so his Chapter 18, “Outguessing Big Data,” is a must read. In this age of plastic, your cell phone carrier, bank, cable company, etc., know everything about you, including the likelihood that you might switch to a competitor who is about to have an alluring blitz campaign.
You’ve probably gotten weird calls…The call means that an algorithm has predicted that you are likely to “churn” (cancel your service)…you’ll be presented with the so-called primary offer…Never accept a primary offer. Once you reject it, the caller will bring up the secondary offer. It’s all in the script. Sometimes the second offer is better; other times it’s just different…You can always reverse yourself and ask for the first after hearing the second. A still better strategy is to reject all offers. Wait a few days and then call to cancel the service. (Do this even if you intend to keep it).
Another technique for outguessing Big Data is to phone the large corporation via Google Voice because
Your Internet phone number is likely to have less data attached to it than your main number…This time the software will see your Internet phone number, not your regular one…Companies want new customers, so they are unlikely to lump blank slate numbers in with the bad apples.
Discussion
1. From this article by Mark Nigrini, we find
Digit |
First digit frequency |
Second digit frequency |
|---|---|---|
| 0 | --- | 0.11968 |
| 1 | 0.30103 | 0.11389 |
| 2 | 0.17609 | 0.10882 |
| 3 | 0.12494 | 0.10433 |
| 4 | 0.09691 | 0.10031 |
| 5 | 0.07918 | 0.09668 |
| 6 | 0.06695 | 0.09337 |
| 7 | 0.05799 | 0.09035 |
| 8 | 0.05115 | 0.08757 |
| 9 | 0.04576 | 0.08500 |
Regarding applicability of the law, the article has this to say.
Not all data sets are expected to have the digit frequencies of Benford’s Law: therefore, the guidelines for deciding whether a data set would comply are that:
- The numbers in the data set should describe the sizes of the elements in the data set.
- There should be no built-in maximum or minimum to the numbers. A maximum or minimum that occurs often would cause many numbers to have the digit patterns of the maximum or minimum.
- The numbers should not be assigned. Assigned numbers are those given to objects to identify them. Examples are social security, bank account, and telephone numbers.
Benford's Law can be generalized to later digits. See here for the distribution of the first through fifth digits. The leading digit is never a zero, but subsequent digits approach a uniform distribution on {0,1,...,9}, each appearing with probability 1/10.
2. Poundstone’s Chapter 22, “How to Outguess the Stock Market,” is his longest chapter and perhaps the most puzzling. Here we are potentially dealing with real money, namely yours. He is enamored with the Shiller PE ratio and is quite emphatic, without the usual “the past may not be an indicator of future performance” hedge.
For still better returns,…When the Shiller PE rises above 24, check the market monthly and sell whenever the market falls 6 percent or more from a recent high. Keep the proceeds in fixed income investments. Then, when Shiller PE falls below 15, check the market monthly and buy back into the market whenever the PE rises 6 percent or more from a recent low.
3. Unfortunately, Poundstone seriously misleads when he naively cites the many behavioral economic studies which say, more or less, that the average of one (convenient) group (of university students) is different from another (convenient) group (of university students). Without referring to variability between the groups, the average difference is virtually meaningless. In addition, even if the difference is significant (statistically and practically), it is quite a leap to infer that this difference involving university students at MIT and the University of Chicago applies to all of humankind spatially and temporally.
Submitted by Paul Alper
Micromorts
Margaret Cibes sent a link to the following:
Risk is never a strict numbers game
by Michael Blastland and David Spiegelhalter, Wall Street Journal, 18 July 2014
Noting that people are notoriously bad at weighing risks (e.g., in preferring driving to flying), this essay explains the use Micromorts to simplify comparisons. This unit of measure, representing deaths per million, is credited to Stanford professor Ronald Howard.
David Spiegelhalter, one of the article's authors, is member of the Understanding Uncertainty project, based at the Statistical Laboratory in the University of Cambridge. In one blog post there, entitled Micromorts, horses and ecstasy, he analyzed the controversial claim by a government official that horse riding and using the drug ecstasy have comparable risks. Indeed, as measured in micromorts, this appears to be plausible, but Spiegelhalter explains why the issues at play go beyond crunching the numbers.
For more on micromorts, see
- Understanding uncertainty: Small but lethal
- by David Spiegelhalter and Mike Pearson, Plus magazine, 12 July 2010