Objectives
By physically generating the data
and by calculating the same statistic themselves for each of
several samples, students will understand intuitively that a
statistic’s value varies from sample to sample, and that the
distribution of the statistic’s values is different from the
distribution of the original observations. By comparing the shape,
center, and spread of the (non-normal) distribution of the
original observations to the corresponding features of the
sampling distribution from samples of two different sizes,
students will discover the Central Limit Theorem’s description of
the sampling distributions of the sample mean and sample
proportion.
Materials and
equipment
 |
One
fair six-sided die. (Several dice will speed up the
process and reduce the tedium somewhat.) |
 |
One
penny. (Pennies minted in the early 1960’s have the
most severely beveled edges and are ideal.) |
 |
Data
on a quantitative variable and a categorical variable for
all members of a small population. (The SAT math
scores and the home state for incoming new students at
Wittenberg University in 1995 are provided.
Instructors are encouraged to replace these data with data
of more local interest.) |
Time involved
 |
30
minutes out of class for each of the two
activities |
 |
20
minutes in class for each of the two
activities |
Activity
description - Classroom analysis of sample means
Students should start with a
histogram of the individual observations (i.e., individual dice
rolls), noting that the shape is non-normal, that the mean is
about 3.5, and that the standard deviation is about 1.7. (Students
who have learned how to calculate the mean and standard deviation
of a probability distribution can be asked to verify these
values.) Students should then be directed to consider the
distribution of sample mean values from samples of 4 and 10 dice.
It’s important to display these distributions next to one another
and on the same scale, to lead the students to an understanding of
the effects of sample size on the variability in the sampling
distribution. The following results are from 180 samples,
generated by 36 students.

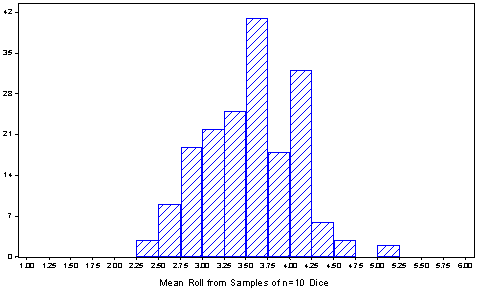
Students quickly recognize that
these sampling distributions are roughly normal, despite the fact
that the distribution of individual rolls was highly non-normal
(namely, uniform). Some simple summary statistics will reinforce
what their eyes tell them about center and spread as well: the
sampling distributions are centered at 3.5, just like the
distribution of individual rolls, but the variability of sampling
distributions decreases with the sample size.
VARIABLE
N
MEAN
SD
MEDIAN
MEAN_4
180
3.5583
0.8059
3.5000
MEAN_10
180
3.5133
0.5214 3.5000
At this point, students can be shown
the simple formula for calculating the standard deviation of the
sample mean’s distribution, and can verify that its prediction
roughly agrees with the standard deviation from their generated
sample means.
To put this information on the sampling
distribution of the sample mean into a more meaningful context,
students are also asked to repeatedly sample from a tangible
population. Given on the student’s
version of the activity are the SAT Math scores for all 398
new students entering Wittenberg University in 1995 who reported
such scores (as opposed to ACT scores alone). Now that they’ve
encountered the Central Limit Theorem, students should try to
anticipate the distribution of the sample means that they have
collected – specifying the shape, center, and spread. To make
these predictions, students will need to know that the population
mean and standard deviation for individual scores are 554.1 and
100.2, respectively.
At that point they can pull up the
data file compiled by the instructor to check their predictions.
Most effective is a visual comparison, on the same scale, of the
distribution of individual scores and the distribution of their
sample means:


Students can easily verify – from
the histograms and from descriptive statistics – that the sampling
distribution of their sample means is centered at roughly the same
place as the distribution of individual scores, but that the
standard deviation is indeed much smaller.
Activity description -
Classroom analysis of sample
proportions
Students should
again start with the distribution of individual observations
(i.e., penny spins) and note that it makes no sense even to
consider shape, center, and spread of a categorical variable’s
distribution. Students should then be directed to consider the
distribution of sample proportion values from samples of 10 and 20
spins. Once again, it’s important to display these distributions
on the same scale, to lead the students to an understanding of the
effects of sample size on the variability in the sampling
distribution. The following results are from 205 samples,
generated by 41 students.


Again, students quickly recognize
that these sampling distributions are roughly normal, despite the
fact that the original variable is not even quantitative, let
alone normally distributed. Here, too, some simple summary
statistics will reinforce what their eyes tell them about center
and spread as well: the sampling distributions are centered at
about 0.4, which is roughly the proportion that most spun pennies
will land heads up, and the variability of sampling distributions
decreases with the sample size.
VARIABLE
N
MEAN SD
MEDIAN
PROP_H_10
205
0.3576 0.1683
0.4000
PROP_H_20
205
0.3712 0.1482
0.3500
At this point, students can be shown
the simple formula for calculating the standard deviation of the
sample proportion’s distribution, and can check whether its
prediction roughly agrees with the standard deviation from their
generated sample means.
In this case, the observed standard
deviations are larger than predicted, which is almost certainly
due to the fact that the pennies used by these classes were minted
in different years and hence have different probabilities of
landing heads-up. For this very reason, Scheaffer et al.
(Activity-Based Statistics, 1996, p.129) recommend that all
pennies used be minted in the same year. If students use pennies
from different years, as was the case with the above results, have
the students report the year each penny was minted, so that they
can then construct a scatterplot of their sample proportions
against minting year:

Although this has nothing to do with
sampling distributions or the Central Limit Theorem, it may be of
interest to see that the probability of landing heads-up has
indeed risen considerably since the early 1960’s, due to changes
in the subtle angle at which the edges are beveled to help the
pennies fall easily out of the minting trays.
If this
differing probability of landing heads-up is a concern, and if
it’s not feasible to have all students use pennies from the same
minting year, instructors can consider alternative experiments
with dichotomous outcomes. One alternative is to flip or drop
thumbtacks and note what proportion land point-up – though
students would need to be given identical tacks, so that the
probability of landing point-up would be the same for all flips.
Another alternative, described by Richardson,
Curtiss, and Gabrosek (2002), is to toss Hershey’s Kisses,
presumed to be of uniform size and shape, and note what proportion
land on the base.
To put this information on the sampling
distribution of the sample proportion into a more meaningful
context, students are then asked to do repeated sampling from a
tangible population. Given is the home state for each of the 610
new students entering Wittenberg University in 1995. Before
looking at the distribution of their sample proportions, students
should be asked to use their new-found theoretical result to
anticipate the shape, center, and spread of this sampling
distribution, and to sketch this distribution. To make these
calculations, students will need to know that 383 of all 610
students are from Ohio, so that the population proportion is
0.628, and hence the sampling distribution of the sample
proportions should be approximately N(0.628, 0.108). Students then
check the accuracy of these predictions. Below is a histogram
based on 117 samples collected by 39 students:
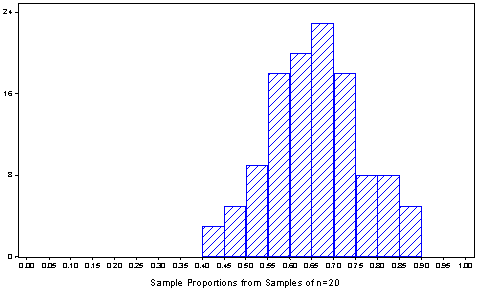
The shape is clearly normal, and the
mean and standard deviation of these particular 117 values of the
sample proportion are 0.633 and 0.106, respectively, which match
the theoretical predictions almost perfectly.
Teacher
notes
Most students will not understand
the idea of a sampling distribution unless they themselves carry
out repeated sampling and calculate the desired statistic from
each of several samples. Merely presenting results collected by
the instructor or results simulated by computer will not reach
many students. Hence students should be required to do the
sampling themselves, ideally in some familiar
context.
Unfortunately, it often takes several dozen
samples before a statistic’s sampling distribution emerges
recognizably; students are understandably reluctant to believe
that a generated sampling distribution is normally distributed
when looking at the statistic’s values from a dotplot of a mere 10
or 15 samples. It helps, then, to pool the sampling energies of
the entire class. Even if the class section is large (say, over
100 students) and a single sample’s result from each student would
suffice to make a convincingly smooth sampling distribution,
however, there is pedagogical benefit to requiring each student to
generate more than one sample each: students then get first-hand
experience with the variability in a statistic’s values in
repeated sampling. Students will, of course, justifiably resent
the tedium if we force them to generate a large number of samples
or if the measurement process is very time-consuming, so these
activities require only three samples each of 4 and 10 dice rolls,
10 and 20 penny spins, and 20 or 25 individuals from a known
population of a few hundred individuals. And in each case, the
statistic calculated from each sample takes only seconds to
calculate.
To save valuable contact time for getting
insight from the sample results, the actual sampling should be
done outside of class, and the instructor should combine the
results into a single data file in preparation for class as well.
The assignment can be given two class sessions before the target
class session and students can hand in their results at the
session before the target session, or the assignment can be given
in the penultimate session and the results submitted
electronically by a deadline chosen to give the instructor time to
consolidate the results.
Assessment
Students should be able to
articulate what is meant by a sampling distribution, both in the
abstract and in a given context. Moreover, students should be able
to use the Central Limit Theorem to predict the sampling
distribution of the sample mean and sample proportion, both in the
abstract and in a given context. As an optional reinforcing
activity, students can examine the sampling distribution of a
simple statistic from repeated sampling on some aspect of their
class.
- What do we mean by a “sampling
distribution”?
- Which of the following have sampling
distributions: variables, parameters, statistics, data,
individuals?
- What does the Central Limit Theorem tell you
about the sampling distributions of the sample mean and sample
proportion?
- The weight of chicken eggs varies with a mean
of 56g and a standard deviation of 6g. Eggs are packed in
cartons by the dozen. Describe in context the relevant sampling
distribution. What does the Central Limit Theorem predict for
this sampling distribution? Sketch the distribution of
individual egg weights, and sketch the relevant sampling
distribution on a separate graph using the same
scale.
- Suppose 15% of the incoming students at this
college are left-handed, and that students are assigned in
groups of 25 to freshman advisors. Describe in context the
relevant sampling distribution. What does the Central Limit
Theorem predict for this sampling distribution? Sketch the
relevant sampling distribution.
- Gather the heights (in cm) of all students in
the class. Make a visual display of this distribution, and
report measures of center and spread. Take 100 samples of 5
students each and calculate the mean height of each sample. Make
a visual display of these sample mean heights, and report
measures of center and spread. What does the Central Limit
Theorem predict for this sampling distribution? How close are
the its predictions to your actual sampling
distribution?
References
Richardson,
M., Curtiss, P., and Gabrosek, J. (2002). “What is the
Significance of a Kiss?” Statistics Teaching and Resource
Library [on-line]. March 17.
Scheaffer, R.,
Gnanadesikan, M., Watkins, A., and Witmer, J. (1996).
Activity-Based Statistics. New York:
Springer.