|
The applet in this section allows you see how probabilities are determined from the exponential distribution.
The exponential distribution is a continuous probability distribution and is quite often used to model rates of decay or growth or to model waiting times in a Poisson process.
The exponential distribution is completely specified by one parameter: the rate, 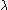 .
The parameter .
The parameter 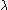 must be strictly positive.
Due to limitations of screen size, the applet restricts must be strictly positive.
Due to limitations of screen size, the applet restricts 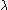 to values between 0.2 and 5, inclusively. to values between 0.2 and 5, inclusively.
For a random variable defined by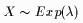 , the probability density function (p.d.f.) is given by , the probability density function (p.d.f.) is given by
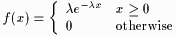 . . | (1) |
The cumulative distribution function (c.d.f.) is determined by integrating (1):
 . . | (2) |
Table 1 contains all the details for the exponential distribution.
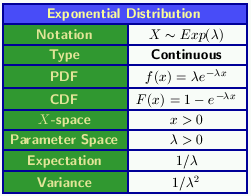
|
|
Table 1. Details of the Exponential distribution.
|
The applet determines any of the three following probabilities from (2) for given 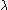 : :
Note: The Central Limit Theorem applet defines the exponential distribution using the parameter 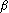 .
In that case .
In that case 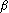 is the mean of the exponential distribution rather than the rate, is the mean of the exponential distribution rather than the rate, 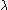 .
The two notations are equivalent by letting .
The two notations are equivalent by letting 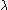 =1/ =1/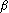 . .
See also: Probability Distributions, Normal Distribution, T Distribution.
|