|
Correlation is a measure of the linear relationship between two random variables X and Y.
The population correlation coefficient is defined by
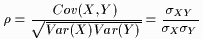 | (1) |
where Cov() represents covariance and Var() represents variance.
The covariance between X and Y is defined by
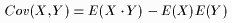 | (2) |
where E(X) and E(Y) are the expectations (population means) of the random variables X and Y, respectively.
The correlation defined in (1) is scale-independent (i.e. no units) and ranges from -1 to +1.
Four important interpretations of (1) are given below:
- A correlation of -1 or +1 implies a perfect linear relationship between X and Y: Y = cX, for some constant c.
- A positive correlation implies a positive relationship between X and Y: as X increases, Y increases.
- A negative correlation implies a negative relationship between X and Y: as X increases, Y decreases.
- A correlation of zero implies that there is no linear relationship between X and Y (see below for details).
Note that if X and Y are independent then E(XY) = E(X)E(Y), which makes (2) identically zero.
This implies that independent random variables have a correlation of zero.
However, this is not a two-way statement: A correlation of zero does not imply independence.
Because correlation is a measure of the linear relationship between X and Y, other non-linear relationships (e.g. Y = X2) may result in a correlation of zero.
The population correlation coefficient defined by (1) is estimated by
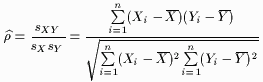 | (3) |
which is called the sample correlation coefficient.
The expression given by (3) is sometimes referred to as Pearson's correlation coefficient.
The applets in this section allow you to see how different bivariate data look under different correlation structures.
The Movie applet either creates data for a particular correlation or animates a multitude data sets ranging correlations from -1 to 1.
The Creation applet allows the user to create a data set by adding or deleting points from the screen.
For either applet, the correlation between X and Y is estimated by (3).
See also: Regression.
|