The applets in this section allow you to see how the common Xbar control chart is constructed with known variance. The Xbar chart is constructed by collecting a sample of size n at different times t. The process is considered to be out of control if the sample mean of the current sample falls above or below the control limits. The upper and lower control limits (UCL & LCL) for target mean and variance known are defined by

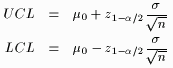(1)

The value in (1) represents the probability of our process giving a false alarm (signaling when no problem exists). In hypothesis testing a false alarm is simply a Type I error. For = 0.0027, the z-scores in (1) are simply the number 3, leading to the 3-sigma control limits defined by

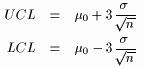
We will also define the average run length (ARL) as the expected number of time periods we have before our chart signals (i.e. sample mean is above UCL or below LCL). To determine the ARL we have the following function

(2)

which is the same as the calculation for Power for a two-tailed hypothesis. For 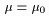, (2) reduces to 0.0027, the probability of a false alarm. The ARL of an Xbar chart is defined as

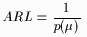(3)

Thus, combining (2) and (3) we see that for = 0.0027, our ARL = 1/0.0027 = 370.4. This means that on average we should expect a false alarm every 370 time periods. Under the above conditions, what would the ARL be if we kept = 0.05, the typical value used in hypothesis testing?

From (2) we see that the three parameters that affect our ability to detect when the process is out of control are:

1. , the difference in the target mean and the process mean (possibly zero, if process is in control),
2. n, the sample size, and
3. ², the variance of the process.

The following applets fix the true mean to be 10.0 while the above parameters can be changed. The applets are designed so that the process mean can be changed at t = 15.