The applets in this section allow you to see how levels of confidence are achieved through repeated sampling. The confidence intervals are on p, the probability of a success in a binomial experiment (e.g. coin flip). In a binomial experiment we are interested in estimating = P(success). Our estimate for is

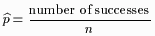(1)

For sufficiently large n, and min[n,n(1-)]>5 then (1) has an asymptotically normal distribution given by

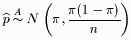(2)

Using the distribution in (2) we can construct a (1-)100% confidence interval by

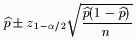(3)

The three parameters that effect the width of the confidence interval in (3) are:

1. n, the sample size,
2. the size of , and
3. the size of , the level of confidence.

As noted above, the reliability of the confidence interval is dependent upon the size of n and . The following applets allow you to change each parameter either separately or simultaneously.

For each applet, x will denote the number of successes out of n independent Bernoulli trials. Each time the Compute! button is pressed, 25 new samples are created for specified n, , and confidence level. You should expect to see approximately (1-)100% of the intervals capturing the true value of .