Stability Testing
The Food and Drug Administration (FDA) requires pharmaceutical companies to establish a shelf life (expiration date) for all new drug products. Pharmaceutical companies perform a stability analysis to determine how stable a drug is over time. Regression models allow pharmaceutical companies to determine the stability of the drug and establish a shelf life.
Millard Pharmaceuticals wants to determine the shelf life of their new drug, CBM. A random sample of the drug in tablet form is placed into storage at 25°C±2°C and 60%±5% relative humidity. At the time intervals: 3, 6, 9, 12, 15, 18, 21, 24, 30, 36, 48, and 60 months, a randomly selected tablet is taken out of storage and measurements are made upon it. One of the measurements for each tablet is the potency (strength) of the drug expressed as a percent of Millard's claim. For example, a value of 99% implies the potency of the tablet is 99% of what Millard claims it to be. Millard is required to keep the potency level between 95% and 105% of their claim. This ensures consumers will take a drug with the desired level of potency. Below is the data collected.
|
Time |
Potency |
|
3 |
99.0% |
|
6 |
102.0 |
|
9 |
98.0 |
|
12 |
98.5 |
|
15 |
97.5 |
|
18 |
96.0 |
|
21 |
96.5 |
|
24 |
96.1 |
|
30 |
95.2 |
|
36 |
95.0 |
|
48 |
94.0 |
|
60 |
95.1 |
Answer the following questions. Show your calculations to receive full credit.
1) Using time as the independent variable and potency as the dependent variable, fit the simple linear regression model in a software package and hand-in the regression output.
2) What is the estimated regression model?
3) Is there a significant linear relationship between potency and time? Perform a hypothesis test to determine this with a type I error rate of 0.05.
4) What is R2? What does this suggest about how well the estimated regression model fits the data?
5) Predict the potency level for a time of 10 months.
6) In #5, what is the 95% confidence interval for the mean potency? Interpret the meaning of the confidence interval. Make sure to show any by-hand or computer calculations.
7) In #5, what is the 95% prediction interval for the predicted potency? Interpret the meaning of the prediction interval. Make sure to show any by-hand or computer calculations.
8) What is the shelf life of CBM? To obtain the answer, perform the following steps and turn in your plot:
a) Construct a scatter plot of the data.
b) Plot the estimated regression line on the scatter plot.
c) Plot the 95% confidence interval and prediction interval bands for the potency on the scatter plot.
d) Plot horizontal lines at 95% and 105% potency levels.
e) The shelf life is the smallest time in which the 95% confidence interval bands intersect the 95% or 105% potency lines.
9) The FDA requires 95% confidence intervals bands to be used to find the shelf life. What is the shelf life if 95% prediction interval bands are used instead?
10) Discuss the difference between what confidence intervals and a prediction intervals estimate in terms of finding the shelf life. What are some instances in which a confidence interval is more appropriate than a prediction interval and vice-versa? Should the FDA use confidence intervals or prediction intervals? Explain.
11) Using the method in 8), what happens to the estimated shelf life when the confidence level decreases? Explain your answer.
12) Would someone receiving the drug prefer a lower or higher level of confidence when the shelf life is determined? Explain your answer (your answer to 11 will help).
13) Would the drug company prefer a lower or higher level of confidence when the shelf life is determined? Explain your answer (your answer to 11 will help).
Prototype Activity Answer Key
1) Excel regression output:
|
SUMMARY OUTPUT |
|
|
|
|
|
|
||
|
Regression Statistics |
|
|
|
|
|
|||
|
Multiple R |
0.7967 |
|
|
|
|
|
||
|
R Square |
0.6348 |
|
|
|
|
|
||
|
Adj. R Square |
0.5983 |
|
|
|
|
|
||
|
Standard Error |
0.0141 |
|
|
|
|
|
||
|
Observations |
12 |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
||
|
ANOVA |
|
|
|
|
|
|
||
|
|
df |
SS |
MS |
F |
Sign. F |
|
||
|
Regression |
1 |
0.0034 |
0.0034 |
17.38 |
0.0019 |
|
||
|
Residual |
10 |
0.0020 |
0.0002 |
|
|
|
||
|
Total |
11 |
0.0054 |
|
|
|
|
||
|
|
|
|
|
|
|
|
||
|
|
Coefficients |
Stand. Error |
t Stat |
P-value |
Lower 95% |
Upper 95% |
||
|
Intercept |
0.9931 |
0.0070 |
140.96 |
7.93E-18 |
0.9774 |
1.0088 |
||
|
Time |
-0.0010 |
0.0002 |
-4.17 |
0.0019 |
-0.0016 |
-0.0005 |
||
|
|
|
|
|
|
|
|
||
|
RESIDUAL OUTPUT |
|
|
|
|
|
|
||
|
Observation |
Pred. Potency |
Residuals |
|
|
|
|
||
|
1 |
0.9900 |
0.0000 |
|
|
|
|
||
|
2 |
0.9869 |
0.0331 |
|
|
|
|
||
|
3 |
0.9839 |
-0.0039 |
|
|
|
|
||
|
4 |
0.9808 |
0.0042 |
|
|
|
|
||
|
5 |
0.9778 |
-0.0028 |
|
|
|
|
||
|
6 |
0.9747 |
-0.0147 |
|
|
|
|
||
|
7 |
0.9716 |
-0.0066 |
|
|
|
|
||
|
8 |
0.9686 |
-0.0076 |
|
|
|
|
||
|
9 |
0.9624 |
-0.0104 |
|
|
|
|
||
|
10 |
0.9563 |
-0.0063 |
|
|
|
|
||
|
11 |
0.9441 |
-0.0041 |
|
|
|
|
||
|
12 |
0.9318 |
0.0192 |
|
|
|
|
||
2)
![]() =0.9931
- 0.0010*Time
=0.9931
- 0.0010*Time
3) Hypothesis test for b1=0:
a) Ho:b1=0
Ha:b1¹ 0
b) p-value = 0.0019
c) a=0.05
d) Since 0.0019 < 0.05, reject Ho
e) There is a linear relationship between time and potency.
4) R2=0.6348. 63.48% of the variation in potency is explained by time.
5)
![]() =0.9931
+ -.0010*10 = 0.9831
=0.9931
+ -.0010*10 = 0.9831
6) 0.9712 £ E(Y) £ 0.9945
7) 0.9494 £ Y £ 1.0163
8) Approximately 32 months
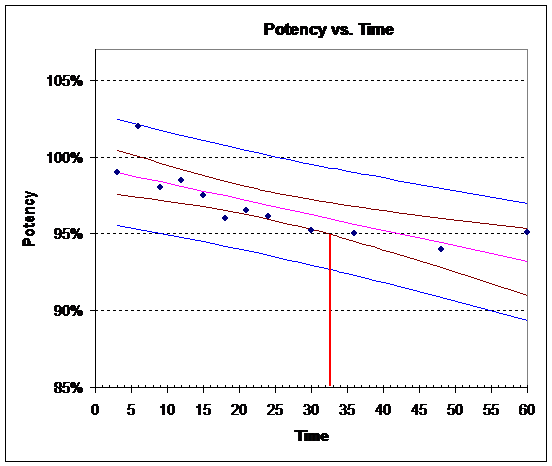
9) Approximately 9 1/2 months
10) Confidence intervals estimate the mean potency of the tablets and allow for the finding of the average shelf life. Prediction intervals estimate the potency for a tablet and allow for the finding of the shelf life of a tablet. If a person takes the drug many times (many tablets), a confidence interval would be more appropriate because the person may be more interested in the average potency. This may be the case for someone taking medication for a chronic disease. If a person takes the drug only once, the prediction interval would be more appropriate. This may be the case for a drug given to an individual once in an emergency room. Potency is considered a random variable here instead of a parameter.
11) Increases since the confidence interval band will “hug” the estimated regression line closer. Thus, the intersection of the lower confidence interval bound will happen later in time. For example, the plot below uses a=0.20 (80% confidence).
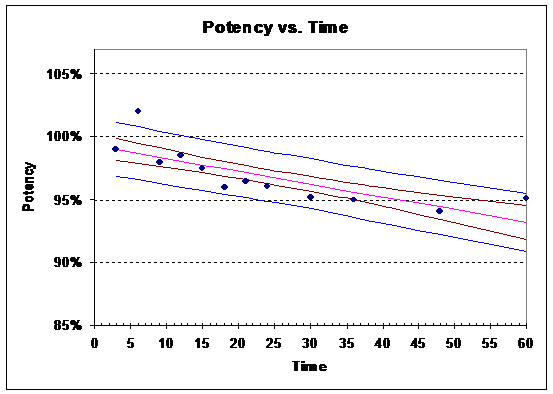
12) Probably a higher level of confidence since there is more “confidence” that the drug being taken is at the required potency level.
13) Probably a lower level of confidence since the drug will have a longer shelf life. Since the drug will stay on the shelf longer, less of the “expired” drug will need to be taken off the shelf. Another way to answer the question is that the drug company would want a higher level of confidence. The company would have more “confidence” that their customers are taking the drug at the correct potency level.