What Is The Significance Of A Kiss?
Purpose:
This activity is intended to illustrate properties of hypothesis testing and to describe how to perform hypothesis tests on a proportion.
Statistical Guide: (Aliaga and Gunderson 1999)
We want to test hypotheses about the population proportion p. The null hypothesis is Ho:p=po, where po is the hypothesized value for p. The data are assumed to be a random sample of size n from the population, where n is large (n must be large enough so that npo³5 and n(1-po)³5). From the sample data, we calculate the sample proportion
![]() .
.
We base our decision about p on the standardized sample proportion
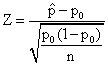 .
.
This z-score is the test statistic and its distribution under Ho is approximately N(0,1).
We calculate the p-value (observed level of significance) for the test, which depends on how the alternative hypothesis is expressed:
(1) If Ha:p>po, then the p-value is the area to the right of the observed test statistic under the Ho model.
(2) If Ha:p<po, then the p-value is the area to the left of the observed test statistic under the Ho model.
(3) If Ha:p¹po, then the p-value is the sum of the area to the left of negative the absolute value of the observed test statistic and the area to the right of the absolute value of the observed test statistic under the Ho model.
The p-value is the probability, computed under the assumption that Ho is true, of obtaining a test statistic value at least as favorable to Ha as the value that actually resulted from the data. Ho is rejected if the p-value is small enough.
Rejecting the null hypothesis when in fact it is true is called a Type I error. The significance level, a, is the chance of committing a Type I error. Ho is rejected if the p-value £ a.
Failing to reject the null hypothesis when in fact it is not true is called a Type II error. The chance of committing a Type II error is b. The chance of rejecting the null hypothesis when in fact it is false is called the Power. The Power of a test is 1-b.
Instructions:
Each person should have 10 plain KISSES® chocolates, a 16-ounce plastic cup, and two sticky notes.
Examine one of the KISSES® chocolates. There are two possible outcomes when a KISSES® chocolate is tossed - landing completely on the base or not landing completely on the base.
Estimate p, the proportion of the time that a KISSES® chocolate will land completely on its base when
tossed: (circle one)
p is approximately 50% p < 50%
The investigation is as follows:
Put 10 KISSES® chocolates into the cup; and:
· Gently shake the cup twice to help mix up the candies.
· Tip the cup so the bottom of the rim is approximately 1-2 inches from the table and spill the candies.
· Count the number of candies that land completely on their base.
· Return the candies to the cup and repeat until you have spilled the candies 5 times.
Record your results on the Data Table.
Data Table:
|
Toss Number |
Number of Candies Landing Completely on Base |
|
1 |
|
|
2 |
|
|
3 |
|
|
4 |
|
|
5 |
|
|
Total |
|
Questions:
Throughout answering the following questions, assume that the true value of p = .35. This value is based on previous experience with tossing plain KISSES® chocolates.
1. Test Ho:p=.5 versus Ha:p<.50.
Use p-values (observed significance levels) to perform the tests. Take calculations to two significant digits. Note: Ho is false. A correct decision would be to reject Ho. An incorrect decision would be to fail to reject Ho. (This would be a Type II error.)
(a) Use all of your data for the tosses (n = 50) and a 5% level of significance (a = .05).
calculated test statistic =
p-value =
(Write your p-value on a sticky note and place it on the stem-and-leaf plot labeled Question 1.)
decision =
P(Type II error) = b. For the class b =
Power =1-b. For the class 1-b =
(b) Use all of your data for the tosses (n = 50) and a 20% level of significance (a = .20).
calculated test statistic =
p-value =
decision =
P(Type II error) = b. For the class b =
Power = 1-b. For the class 1-b =
(c) Explain, using complete sentences, how to interpret a Type II error rate in terms of repeatedly performing the procedure of selecting a sample and using the sample data to test a hypothesis about a population parameter.
(d) Explain, using complete sentences, how the Type I error rate (a) is related to the Type II error rate (b). In addition, give an intuitive explanation as to why this relationship holds.
2. Test Ho:p=.35 versus Ha:p¹.35.
Use p-values (observed significance levels) to perform the tests. Take calculations to two significant digits. Note: Ho is true. A correct decision would be to fail to reject Ho. An incorrect decision would be to reject Ho. (This would be a Type I error.)
(a) Use all of your data for the tosses (n = 50) and a 5% level of significance (a = .05).
calculated test statistic =
p-value =
(Write your p-value on a sticky note and place it on the stem-and-leaf plot labeled Question 2.)
decision =
expected number of rejections of Ho for the class =
number of rejections of Ho for the class =
(b) Use all of your data for the tosses (n = 50) and a 20% level of significance (a = .20).
calculated test statistic =
p-value =
decision =
expected number of rejections of Ho for the class =
number of rejections of Ho for the class =
(c) Explain, using complete sentences, how to interpret a Type I error rate in terms of repeatedly performing the procedure of selecting a sample and using the sample data to test a hypothesis about a population parameter.
Stem-and-leaf plot for class p-values:
.0|
.0|
.1|
.1|
.2|
.2|
.3|
.3|
.4|
.4|
.5|
.5|
.6|
.6|
.7|
.7|
.8|
.8|
.9|
.9|
1 |
Answers to Activity Questions and Assessment Questions:
Activity Questions.
1.
(c) If we repeatedly perform the procedure of selecting a sample and using the sample data to test a hypothesis about a population parameter, the Type II error rate is the percentage of the samples that would lead us to fail to reject a false null hypothesis.
(d) The Type I error rate is inversely related to the Type II error rate. If, for instance, we decrease the Type I error rate, we are making it more difficult to reject the null hypothesis, which in turn will increase the chances of failing to reject a false null hypothesis; therefore increasing the Type II error rate.
2.
(c) If we repeatedly perform the procedure of selecting a sample and using the sample data to test a hypothesis about a population parameter, the Type I error rate is the percentage of the samples that would lead us to reject a true null hypothesis.
Assessment Questions.
1.
(a) A Type I error in the context of this problem would be if the parachutist concludes that the parachute will not open when in fact it will open.
(b) A Type II error in the context of this problem would be if the parachutist does not conclude that the parachute will fail to open when in fact it will fail to open.
(c) A Type II error is far worse in this situation. A Type I error would lead the parachutist either not to jump or to get a new parachute, when the parachute she has is actually fine. The only loss would be time and or minimal financial loss. A Type II error would lead to the parachutist jumping and the parachute failing to open. This would mean serious injury or death.
(d) The back-up guards against Type II error. If the parachutist jumps and the rip cord fails to open the parachute, then she can employ the back-up and still land safely.
(e) If you were concerned about a Type I error you would pull the rip cord again. You wouldn't want to conclude the rip cord will fail when it will actually work. If you were concerned about a Type II error you would pull the back-up. You wouldn't want to fail to use the back-up if the rip cord is truly malfunctioning. I'd pull that back-up. You've already tried the rip cord and it failed to deploy the parachute. I'm not about to give it another chance.
2.
(a) Type I error and Type II error are inversely related. Thus, if you increase the Power of a test (thereby decreasing the chance of a Type II error) this will increase the chance of a Type I error.
(b) If you set the Type I error rate at .0001 then you are increasing the chance of making a Type II error. That is, it will be very hard to reject a false null hypothesis.
3.
Each student has generated a value
for ![]() .
A histogram of these values is an approximation to the distribution of the
sample proportion
.
A histogram of these values is an approximation to the distribution of the
sample proportion ![]() .
The mean of these
.
The mean of these ![]() values is an estimate of the mean
values is an estimate of the mean ![]() of the
sampling distribution. The standard deviation of these
of the
sampling distribution. The standard deviation of these ![]() values is an estimate of the standard deviation
values is an estimate of the standard deviation ![]() of the sampling distribution.
of the sampling distribution.
4.
(a) 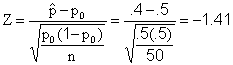
p-value = ![]() =
.0793
Fail to Reject Ho, since .0793 > .05.
=
.0793
Fail to Reject Ho, since .0793 > .05.
(b) 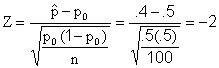
p-value = ![]() =
.0228
Reject Ho, since .0228 < .05.
=
.0228
Reject Ho, since .0228 < .05.
(c) When you use a larger sample size, you decrease the standard error. This makes it easier to reject the null hypothesis.
(d) When the sample size increases, the standard error decreases, which results in the absolute value of the test statistic increasing.
(e) When the sample size increases, the absolute value of the test statistic increases, which results in the p-value decreasing.
(f) As the sample size increases, the probability of a Type II error decreases, and the Power of the test will increase.