Counting Eights: An Introduction to Probability

 

 

 

1.  Warm-Up

 

Roll a pair of dice and record the sum of the dots showing on the dice   ________

 

2.  Estimating the Probability of Rolling an 8

 

(A) In Minitab, give column C1 the name Trial

Task: Make C1 consist of the whole numbers from 1 to 1000.

Select:  Calc > Make Patterned Data > Simple Set of Numbers >

From first value =1 to last value = 1000

 

(B) Give column C2 the name Red Die

Task: Make C2 consist of 1000 rolls of a balanced die

Select: Calc > Random Data > Integer >

Minimum value = 1 and Maximum value = 6

 

(C) Give column C3 the name Green Die

Task: Make C3 consist of 1000 rolls of another balanced die

Select: Calc > Random Data > Integer >

Minimum value = 1 and Maximum value = 6

 

(D) Give column C4 the name Sum of Dice

Task: Make C4 the sum of Red Die and Green Die

Select: Calc > Calculator

 

(E) Give column C5 the name Sum=8?

Task: Make C5 have value 1 if Sum of Dice is 8, and a 0 if Sum of Dice is not 8.

Select: Calc > Calculator, and now type (C4=8) in the Expression box.  Minitab will

recognize this as a logical expression and place a 1 where the expression is true and place

a 0 where the expression is false.

Check to make sure your commands worked as desired.

 

 (F) Give column C6 the name 8s So Far

Task: Make C6 the number of 8s rolled so far in your sequence of rolls

Select: Calc > Calculator, and now type PARS(C5) in the Expression box.  PARS stands

for partial sums.

Check to make sure your commands worked as desired.

 

(G) Give column C7 the name Proportion 8s So Far

Task: Make C7 the proportion of your rolls so far that have been an 8

Select: Calc > Calculator, and now type C6/C1 in the Expression box.

 

(H) What is your value of Proportion 8s So Far at trial number 10?     ________

 

What is your value of Proportion 8s So Far at trial number 25?                       ________

 

What is your value of Proportion 8s So Far at trial number 50?                       ________

 

What is your value of Proportion 8s So Far at trial number 100?                     ________

 

What is your value of Proportion 8s So Far at trial number 500?                     ________

 

What is your value of Proportion 8s So Far at trial number 1000?       ________

 

 

Place dots on the board at the appropriate location for your six numbers above.

 

 

 

Investigations and Questions for Students

 

1. Make a dotplot for the student values of the variable Y at n = 10, 25, 50, 100, 500, and 1000 rolls.  For each dotplot, describe the center, spread, and shape of the distribution.  Now looking over the six dotplots, which distributional characteristics seem to stay constant from plot to plot, and which characteristics appear to be changing from plot to plot?  If a characteristic is changing, explain how it is changing.

 

2. Plot your 1000 values of Y versus roll number n.  Comment on the appearance of the graph and any noticeable trends.

 

3. Consider all the possible pairs of values (red die, green die) when balanced red and green dice are rolled.  Argue why there are 36 equally likely such pairs and use this fact to find 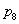, the exact theoretical probability of rolling a sum of 8 when two dice are rolled.

 

4. In problem 3 you found the value of 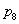, the exact probability of an 8 when two balanced dice are rolled.  Look again at the Y values of the students in your class.  For each value of n = 10, 25, 50, 100, 500, and 1000, what proportion of student Y values

 

(a)    fall within 0.05 of ?

(b)   fall within 0.03 of ?

(c)    fall within 0.01 of ?

 

How does the proportion of Y values falling within a specified range from  

depend on n?  For a fixed small quantity d, what do you think will happen to the

proportion of student Y values within d of  as the number of rolls n gets

increasingly larger?

 

5. If we think of Y as an estimate of the probability 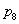, then the relative error of estimation would be

                                                 .

 

For n = 10, 25, 50, 100, 500, and 1000, what proportion of student Y values

provide a relative error of estimation of less than 0.10, or 10%?  How does

this proportion change with n?

 

6. Compare your graph in question 2 with as many of your fellow students as

possible.  Keep in mind that you all have different random simulations and

therefore very different sequences of 1000 rolls.  Which regions of your graph are

similar to those of other students, and which regions of your graph differ from

those of other students?  After your comparisons, complete this sentence:  The

most striking characteristic that is common to my and my fellow students’ graphs

is _________ .  Can you state this apparent law of random behavior in a concise

statement?

 

7. Find the sample standard deviation, 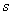, of the student Y values at n = 10, 25, 50, 100, 500, and 1000. 

 

(a)    Plot the six points on a graph, wheredenotes the natural or base e logarithm.  Describe the appearance of this plot.

(b)   Find the intercept and slope  of the least squares regression line through the six points graphed in (a).

(c)    Show that (a) and (b) imply that , where  is a constant. It turns out the theoretical values of  and  are  and .  Compare these theoretical values with your estimates.